Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 15

Из Таблицы 1 видно, что соб­ственное значение  является вырожденным, так как той же критической волной обладает и волна Е₁₁. Это вырож­дение является следствием соотношения (П2.10) для бесселевых функций, благодаря которому x_0n = y_1n (n =1, 2, ...) и все волны Е_1n и H_0n являются вырожденными.

Волна Е₁₁ в круглом волноводе имеет функцию

, , 

 ,

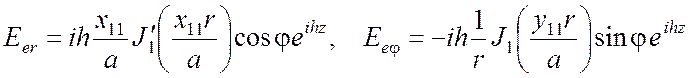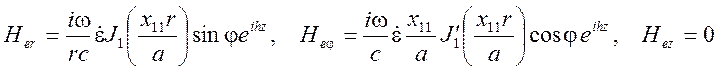,      (3.44)

Линии уровня этой функции изображены на рис. 3.8. Картину этих линий легко построить, если учесть, что на горизонтальном диа­метре, т. е. при  = 0 и , при r < a достигается согласно рис. 3.5  максимум и минимум функции , вблизи которых ли­нии уровня имеют эллиптическую форму. Кроме того, вертикаль­ный диаметр также является линией уровня, так как  = 0 при . Эти линии уровня дают магнитные силовые линии, а электрические линии, им ортогональные, изображены на рис. 3.8 штриховой линией.

Вырождение собственного значения , соответствующе­го волне H₀₁, делает проблему передачи энергии с помощью такой волны довольно трудной, так как при небольших возмущениях формы волновода волна H₀₁ имеет тенденцию превращаться в вол­ну Е₁₁, обладающую той же фазовой скоростью, но гораздо большим затуханием (см. § 3.4). Для волны Е₁₁ имеется диапазон одноволновости 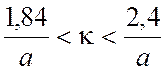. Так как размеры волновода на практике выби­рают обычно так, чтобы при данной частоте в нем могла распро­страняться только одна волна, то область применения круглых волноводов -  сантиметровые и более короткие волны.

3.5. Фазовая и групповая скорости волны

Теория распространения электромагнитных волн в волново­де (см. § 3.1) для электрического и магнитного полей каждой волны дает следующие выражения:

,                             (3.53)

где векторы  и  не зависят от координаты z вдоль волновода, а h есть продольное волновое число распространяющейся волны. Переходя к мгновенным значениям электрического и магнитного полей по формулам (1.15), получаем

, .          (3.54)

Такие волны (при веществен­ном h)распространяются со скоростью

,                                         (3.55)

которая называется фазовой скоростью данной монохроматичес­кой волны (см. § 2.1).

Передача сигналов с помощью монохроматической волны не­возможна из-за ее однородности в пространстве и во времени, поэтому сигнал всегда имеет некоторый спектр частот и распро­страняется со скоростью, вообще говоря, отличной от .

Согласно формулам (1.18) электрическое поле волны, перено­сящей сигнал, представляется в виде

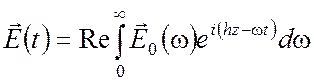,                                       (3.56)

где вектор  кроме частоты  зависит еще от поперечных координат х и у, а продольное волновое число h есть функция частоты. В таком же виде записывается магнитное поле. Ниже мы будем рассматривать какую-нибудь одну составляющую поля при фиксированных значениях х и у, обозначая ее через f(z,t). Вмес­то выражения  (3.56)  используем более удобную запись

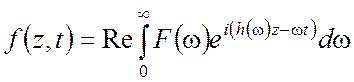 ,                                    (3.57)

в которой явно фигурируют все существенные аргументы рассмат­риваемых функций.

Интеграл (3.57) легко вычисляется, если при всех частотах выполняется равенство , где с — постоянная; такая зависимость h от  реали­зуется для плоских волн в пустоте. Формула (3.57) принимает вид

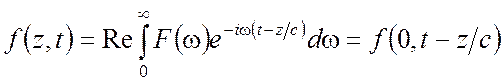.                     (3.58)

В дальнейшем будем называть f (0,t)начальным сигналом, предполагая, что его посылают из точ­ки z = 0, и следить за тем, в каком виде он при­дет в любую точку z  > 0. Формула (3.58) показывает, что при  сигнал распространя­ется без искажения и в точке z > 0 появляется, запаздывая на время z/c, т.е. с есть скорость его распространения.

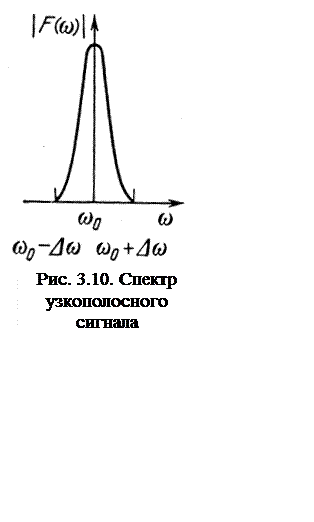
При иной зависимости h от  ситуация усложняется и интег­рал (3.58) так просто не вычисляется. Прибегнем к аппроксима­ции, предполагая, что сигнал узкополосный, имеет достаточно уз­кий спектр, т. е. функция  практически отлична от нуля лишь при (рис. 3.10), где  - несущая частота. Тогда функцию  можно заменить первыми двумя членами ряда Тейлора

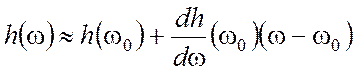                        (3.59)

и                  .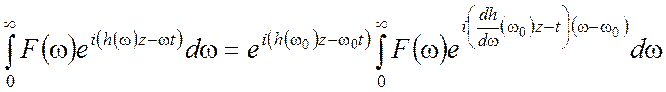

Чтобы понять смысл этого выражения, надо учесть, что узкополосный начальный сигнал f (0, t) всегда задается в виде