Решениями уравнений Максвелла в
криволинейной ортогональной системе координат являются шесть функций ![]() . В ряде случаев удается все эти шесть
функций, входящих в уравнения Максвелла, выразить через две вспомогательные
функции U и V, удовлетворяющие уравнениям второго порядка (волновому
уравнению или уравнению, приводящему к волновому). Это возможно, если уравнения
(1.49) – (1.52)
. В ряде случаев удается все эти шесть
функций, входящих в уравнения Максвелла, выразить через две вспомогательные
функции U и V, удовлетворяющие уравнениям второго порядка (волновому
уравнению или уравнению, приводящему к волновому). Это возможно, если уравнения
(1.49) – (1.52)
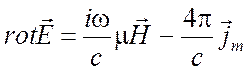 (1.49)
(1.49)
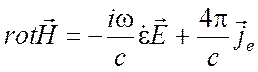 (1.50)
(1.50)
![]() , (1.51)
, (1.51)
![]() , (1.52)
, (1.52)
допускают решения электрического и магнитного типов; тогда функция U однозначно определяет электромагнитное поле электрического типа, функция V - поле магнитного типа.
Решением электрического типа
(или поперечно-магнитным полем) – ТМ - относительно какой-либо координаты ![]() называется такое решение уравнений (1.49)
– (1.52), у которого
называется такое решение уравнений (1.49)
– (1.52), у которого ![]() и
и ![]() ,а решением магнитного типа
(поперечно-электрическим полем) - ТЕ — такое, у которого
,а решением магнитного типа
(поперечно-электрическим полем) - ТЕ — такое, у которого ![]() и
и ![]() .
.
Сформулируем принцип
поляризационной двойственности. В криволинейной ортогональной системе
координат (![]() ), обладающими следующими свойствами:
), обладающими следующими свойствами:
![]() ,
,
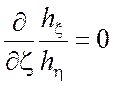 (1.57)
(1.57)
(![]() называется координатой разделения),
решение системы однородных уравнений Максвелла для однородных сред может быть
представлено суперпозицией фундаментальных решений ТМ и ТЕ относительно
координаты разделения
называется координатой разделения),
решение системы однородных уравнений Максвелла для однородных сред может быть
представлено суперпозицией фундаментальных решений ТМ и ТЕ относительно
координаты разделения ![]() . При этом каждое ТМ и ТЕ решение
описывается однокомпонентным электрическим (или магнитным) вектором Герца,
направленным по координате
. При этом каждое ТМ и ТЕ решение
описывается однокомпонентным электрическим (или магнитным) вектором Герца,
направленным по координате ![]() .
.
![]() ,
,
![]() , (1.58)
, (1.58)
где ![]() - единичный орт в направлении
координаты
- единичный орт в направлении
координаты ![]() .
.
Докажем это утверждение. Будем
искать решение системы уравнений Максвелла в виде суммы ![]() ,
,
![]() , таких что каждое из решений
, таких что каждое из решений ![]() ,
, ![]() определяется
через электрический и магнитный векторы Герца
определяется
через электрический и магнитный векторы Герца ![]() и
и ![]() согласно соотношениям (1.56) при
отсутствии источников. Пусть векторы Герца имеют только одну компоненту, т.е.
выполняются соотношения (1.58). Нетрудно убедиться, что в этом случае
выполняются равенства
согласно соотношениям (1.56) при
отсутствии источников. Пусть векторы Герца имеют только одну компоненту, т.е.
выполняются соотношения (1.58). Нетрудно убедиться, что в этом случае
выполняются равенства ![]() и
и ![]() , что
соответствует поперечно-магнитному ТМ и поперечно-электрическому ТЕ полям. Векторы
Герца удовлетворяют однородным уравнениям
, что
соответствует поперечно-магнитному ТМ и поперечно-электрическому ТЕ полям. Векторы
Герца удовлетворяют однородным уравнениям
![]() .
(1.59)
.
(1.59)
Будем искать решения этих уравнений в виде
![]() ,
(1.60)
,
(1.60)
где f - некоторая неизвестная функция. Подставим (1.60) в (1.59) и распишем оператор Лапласа от векторной величины по формуле (П1.6) Приложения 1.
![]() (П1.6)
(П1.6)
Получим уравнение
![]() ,
(1.61)
,
(1.61)
где через ![]() обозначена некоторая
новая скалярная неизвестная функция. Найдем ее. Для этого распишем проекции
уравнения (1.61) в криволинейной ортогональной системе координат (
обозначена некоторая
новая скалярная неизвестная функция. Найдем ее. Для этого распишем проекции
уравнения (1.61) в криволинейной ортогональной системе координат (![]() ) и учтем условия (1.57). Получим систему
уравнений
) и учтем условия (1.57). Получим систему
уравнений
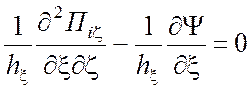 ,
(1.62)
,
(1.62)
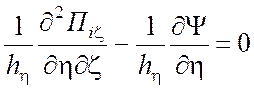 ,
(1.63)
,
(1.63)
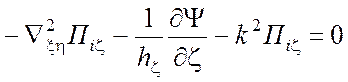 ,
(1.64)
,
(1.64)
где 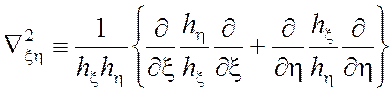 - поперечная часть
оператора Лапласа при
- поперечная часть
оператора Лапласа при ![]() (см. формулу (П1.5) Приложения
1)
(см. формулу (П1.5) Приложения
1)
Интегрируя уравнения (1.62) и
(1.63) по ![]() и
и ![]() соответственно,
получаем выражение для неизвестной функции
соответственно,
получаем выражение для неизвестной функции ![]() в виде
в виде
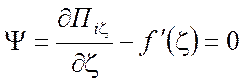 ,
,
и, подставив это выражение в уравнение (1.64), находим
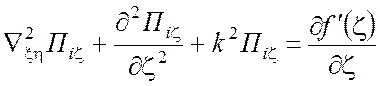
Решение этого уравнения есть ![]() . Так
как выражения для компонент электромагнитного поля инварианты по отношению к
добавлению к вектору Герца произвольной функции
. Так
как выражения для компонент электромагнитного поля инварианты по отношению к
добавлению к вектору Герца произвольной функции ![]() , то эту
функцию можно положить равной нулю. Таким образом, для электрического и
магнитного векторов получаем уравнение
, то эту
функцию можно положить равной нулю. Таким образом, для электрического и
магнитного векторов получаем уравнение
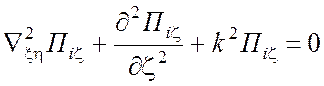 .
(1.65)
.
(1.65)
Компоненты электромагнитного поля находятся из следующих выражений:
для ТМ поля относительно координаты разделения ![]()
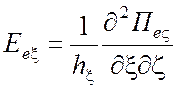 ,
, 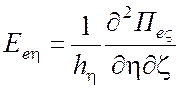 ,
, 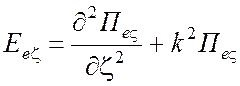 ,
,
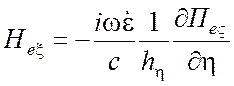 ,
,
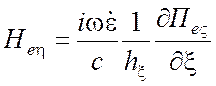 ,
, ![]() (1.66)
(1.66)
для ТЕ поля относительно координаты разделения ![]()
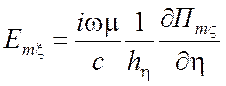 ,
, 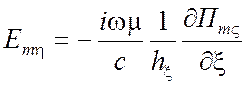 ,
, ![]() ,
,
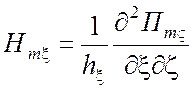 ,
,
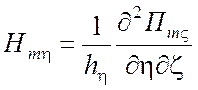 ,
, 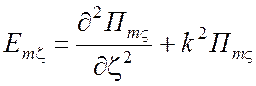 (1.67)
(1.67)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.