Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 23

 на С,                                               (5.7)

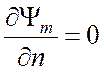 на С.                                            (5.8)

Получим граничные условия для волновых функций q_i(z). Введем вектор нормали  и касательный к боковой поверхности резонатора вектор  так, что орты  образуют правую систему. Тогда касательными к торцевым поверхностям резонатора направлениями будут  и . Из формул (5.5), (5.6) находим тангенциальные компоненты вектора напряженности электрического поля

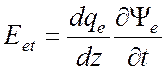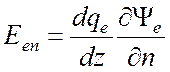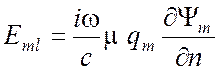, , .               (5.9)

В результате для волновых функций получаем следующие граничные условия:

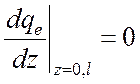,                                                (5.10)

.                                               (5.11)

Таким образом, для электрической волновой функции получили задачу Неймана, а для магнитной – задачу Дирихле.

В качестве линейно независимых решений уравнений (5.4) выберем комбинацию косинусов и синусов

и, удовлетворяя граничным условиям (5.10), (5.11),  приходим к следующим выражениям для волновых функций

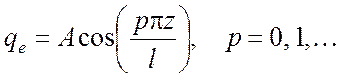,                                  (5.12)

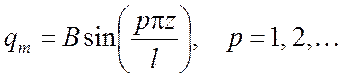 .                                 (5.13)

Здесь имеем дискретный спектр собственных значений электрических и магнитных задач 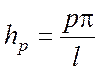. Тогда, учитывая, что для поперечного волнового числа также получается дискретный набор собственных значений , приходим к следующему уравнению

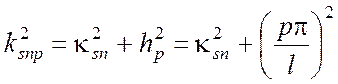.                                    (5.14)

Уравнение (5.14) представляет собой условие резонанса в объемных резонаторах и позволяет определить резонансные частоты . Заметим, что  зависит  от параметров поперечного сечения и длины l .

5.2. Прямоугольный резонатор

Воспользуемся полученными выше результатами и рассмотрим  собственные (или свободные) колебания резонатора простейшей формы, а именно, прямоугольного резонатора, изображенного на рис. 5.1. Выражения для электрических и магнитных мембранных функций были получены в § 3.2 и имеют вид:

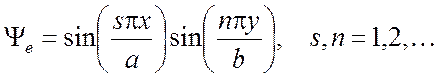,         (5.15)

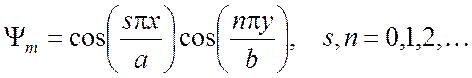     (5.16)

Подставив эти формулы и соотношения (5.12), (514) для волновых функций в уравнения для компонент поля (5.5), (5.6), получим следующие выражения для  поперечно магнитного ТМ поля:

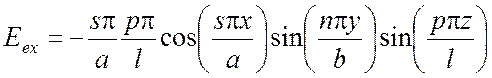,(5.17)

, ,

, ,

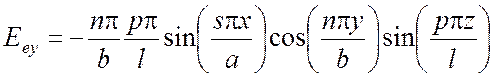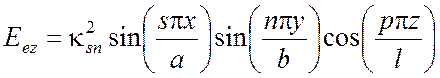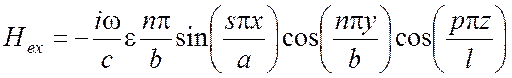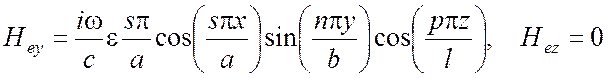Для поперечно электрического поля:

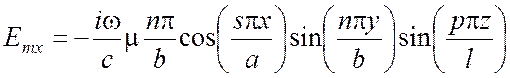,                         (5.18)

,

, , .

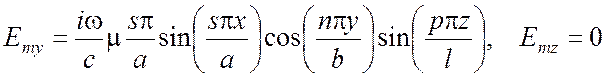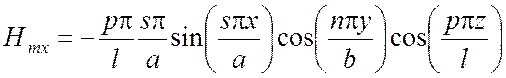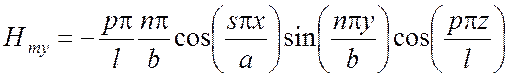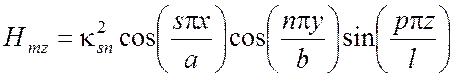Волновое число  определяется по формуле

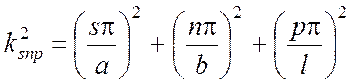 .                           (5.19)

Это значит, что каждой трой­ке чисел s, n и p соответствует собственное колебание, имеющее собст­венную частоту f _snp и собственную длину волны :

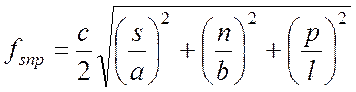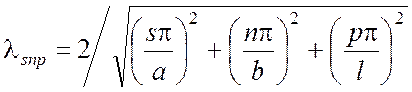,         (5.20)

Если среди чисел s, n и p нет нулей, то такой тройке чисел соответ­ствуют два собственных колебания с одной и той же частотой, но с различной структурой поля - одно элек­тромагнитное колебание, а другое колебание с той же самой частотой, но иным распределением поля.

Если собственной частоте соответствует два или больше соб­ственных колебания, то говорят о наличии вырождения, а данная собственная  частота  называется  вырожденной  или  кратной.  Таким образом, если индексы s, n и p все отличны от нуля, то соот­ветствующая  им собственная частота (5.20) оказывается, по
крайней  мере, двукратно  вырожденной.   Если  размеры  полости а, b, l  являются соизмеримыми, т. е. их отношения являются раци­ональными   числами, то  возможно   вырождение   более   высокой кратности. Так, например, при а = b и  частота (5.20) имеет не менее чем четырехкратное вырождение, поскольку тройкам чисел s, n и p и n, s и p соответствует одна частота, но разные поля.
Если к синусам и косинусам   в формулах   (5.17), (5.18)   применить
формулы Эйлера, то получим комбинацию слагаемых вида

    (5.21)

т.е. согласно § 2.4 сумму плоских волн, распространяющихся в пустоте. Характерная особенность этих плоских волн заключает­ся в том, что на каждом ребре параллелепипеда каждая из этих волн приобретает дополнительную фазу, кратную ; например, при переходе от х = 0 до х = а появляется фазовый множитель  и т. д. В результате сложения этих бегущих плоских волн возникают стоячие плоские волны (5.17), (5.18) с узлами тангенциального электрического поля на стенках.