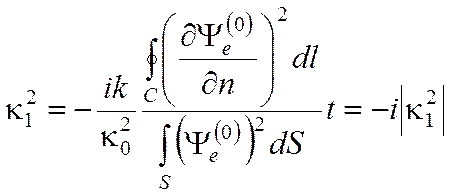Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 20

.                          (4.22)

Действуя аналогично, для поперечно электрического ТЕ поля имеем

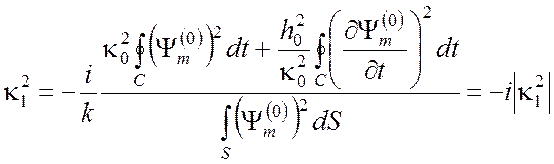.                (4.23)

Наличие двух членов в правой части этой формулы объясня­ется тем, что в магнитных волнах поверхностная плотность тока имеет как продольную составляющую, пропорциональную H_t (второе слагаемое), так и поперечную составляющую, пропорциональную H_z (первое слагаемое). У электрических волн токи текут лишь в про­дольном направлении, и поэтому в фор­муле (4.22) имеется только одно слагаемое.

Рассмотрим продольное волновое число  и воспользуемся малостью параметра Z_m. Тогда, разложив h  в ряд по малому параметру, получаем

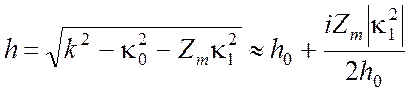,                            (4.24)

где 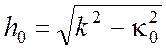 - продольное волновое число в нулевом приближении.

Заметим, что относительное волновое сопротивление Z_m связано с глубиной скин-слоя d соотношением

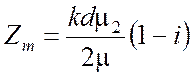,                                        (4.25)

где 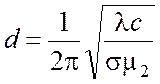.                                         (4.26)

Окончательно, имеем

.                     (4.27)

Здесь введено обозначение для величины , называемой коэффициентом затухания волн в волноводе:

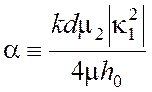.                                           (4.28)

Проанализируем полученные результаты и определим, какую особенность в электромагнитные поля вносит учет конечной проводимости стенок волновода.

Рассмотрим распространяющиеся волны, которые возникают при . В этом случае продольное волновое число является чисто вещественным . Так как электромагнитные поля в волноводе пропорциональны волновой функции , то учет конечной проводимости стенок (наличие отличного от нуля коэффициента ) приводит к следующим результатам:

1) имеет место экспоненциальное затухание амплитуды электромагнитных полей, пропорциональное коэффициенту . Хотя это затухание очень мало вследствие малости , который пропорционален глубине скин-слоя d и обратно пропорционален корню из проводимости ;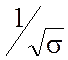

2) учет конечной проводимости стенок приводит к изменению фазы колебаний. Действительно, фазовая скорость в этом случае определяется согласно формуле (3.55) выражением  и, так как  > 0, то .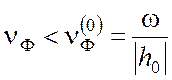

При исследовании местных волн при , когда продольное волновое число является чисто мнимым , помимо большого затухания наблюдается и часть, относящаяся к распространяющимся волнам . Таким образом, теряется абсолютный характер понятий распространяющихся и местных волн.

Проведем качественное исследование зависи­мости коэффициента затухания от частоты. Для этого введем относительную безразмерную частоту

,                                                (4.29)

равную отношению рабочей частоты к критической частоте дан­ной волны. Рассмотрим значение относительной частоты в преде­лах , когда данная волна в идеально проводящем вол­новоде является распространяющейся. Благодаря конечной про­водимости стенок волна приобретает затухание с коэффициентом  (4.28), для вы­числения которого необходимо знать лишь функции  (см. (4.22), (4.23)). Эти собственные функции, равно как и соответствующие им соб­ственные значения , зависят лишь от геометрии волновода и не зависят от частоты. От частоты зависят лишь следующие величины: k (пропорциональна ), h (пропорциональна ) и глубина скин - слоя d (пропорциональна ). В результате получаем

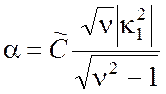.                                           (4.30)

Для электрических волн из формулы (4.22) справедливо

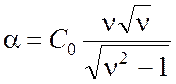,                                            (4.31)

а для магнитных вследствие соотношения (4.23) находим

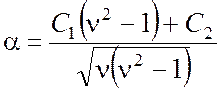,                                     (4.32)

где положительные коэффициенты С₀, С₁и С₂ от  не зависят. Эти формулы показывают, что при стремлении частоты к критической   l, затухание волн неограниченно возрастает и при  = l обращается в бесконечность. Последний вывод является ошибочным и объясняется неприменимостью формулы (4.27) близи критической частоты. Однако при  затухание волн действительно становится аномально большим: оно во много раз больше, чем при более высоких частотах. При больших значениях  формула (4.31) принимает вид , а формула (4.32) приводит к аналогичному соотноше­нию  для магнитных волн. Таким образом, при доста­точно высоких частотах коэффициент затухания возрастает про­порционально квадратному корню из частоты.