Рассмотрим электрические и
магнитные волны в волноводе с круговым поперечным сечением радиуса а или,
кратко, в круглом волноводе. Для решения двумерного волнового уравнения для
мембранной функции (3.7) внутри круглого волновода введем полярную систему
координат r, ![]() с
центром на оси волновода. Уравнение (3.7) примет вид
с
центром на оси волновода. Уравнение (3.7) примет вид
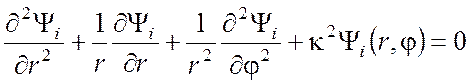 .
(3.35)
.
(3.35)
Для нахождения решения этого уравнения воспользуемся методом разделения переменных и будем искать неизвестную функцию в виде
![]() .
(3.36)
.
(3.36)
Подставив выражение (3.36) в
уравнение (3.7) и разделив его на ![]() , получим уравнения для
функций
, получим уравнения для
функций ![]() и
и ![]() :
:
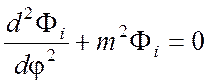 ,
(3.37)
,
(3.37)
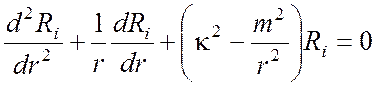 ,
(3.38)
,
(3.38)
где m – константа разделения.
Общее решение уравнения (3.37) представляется в виде
![]() .
.
Так как рассматривается
однородное уравнение (3.37), то без потери общности можно положить начало
отсчета ![]() . Из условия однозначности решения (3.37)
получаем ограничения на константу разделения m, которая
может принимать только положительные целые значения m
= 0, 1, 2, …. В этом случае решение не меняется при повороте угла
. Из условия однозначности решения (3.37)
получаем ограничения на константу разделения m, которая
может принимать только положительные целые значения m
= 0, 1, 2, …. В этом случае решение не меняется при повороте угла ![]() на
на ![]() .
.
Решениями уравнения (3.38) являются цилиндрические функции (см. Приложение 2). В качестве линейно независимых решений (3.38) можно выбрать функции Бесселя (П2.2) и Неймана (П2.6) или Ханкеля (П2.7). Однако, в силу требования конечности решения при r = 0, которому функции Неймана и Ханкеля не удовлетворяют согласно выражению (П2.13), окончательно для мембранной функции получаем выражение:
![]() ,
(3.39)
,
(3.39)
где Сi - постоянная.
Так как функция ![]() должна удовлетворять граничному условию
должна удовлетворять граничному условию ![]() при r = а,
то для поперечного волнового числа
при r = а,
то для поперечного волнового числа ![]() электрических волн в круглом волноводе получаем
уравнение
электрических волн в круглом волноводе получаем
уравнение
![]() .
(3.40)
.
(3.40)
Обозначим n - й положительный корень уравнения Jm(x) = 0 через xmn (см.
формулу (П2.16) Приложения 2), тогда для электрических волн возможны значения ![]() .
Электрическая волна с таким
.
Электрическая волна с таким ![]() , функция
, функция ![]() которой определяется формулой (3.40),
называется волной Етп в круглом волноводе. Функция
которой определяется формулой (3.40),
называется волной Етп в круглом волноводе. Функция ![]() для магнитных волн в круглом волноводе
также должна удовлетворять уравнению (3.7) и поэтому представляется в том же
виде, что и функция
для магнитных волн в круглом волноводе
также должна удовлетворять уравнению (3.7) и поэтому представляется в том же
виде, что и функция ![]() в формулах (3.40). Граничное
условие для нее имеет вид (3.17)
в формулах (3.40). Граничное
условие для нее имеет вид (3.17) 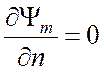 при r = а, поэтому поперечное
волновое число
при r = а, поэтому поперечное
волновое число ![]() магнитной
волны должно удовлетворять уравнению
магнитной
волны должно удовлетворять уравнению
![]() .
(3.41)
.
(3.41)
Если через yтп обозначить
п - й положительный корень уравнения ![]() ,
то возможные значения
,
то возможные значения ![]() для магнитных волн в круглом волноводе имеют вид
для магнитных волн в круглом волноводе имеют вид ![]() . Такое волновое число по определению
соответствует волне Нтп в круглом волноводе. Заметим, что числа xm1, xm2, ... и yт1, yт2, ... образуют возрастающие последовательности,
в которых наибольший интерес представляют числа xm1 и yт1,
соответствующие наименьшим значениям
. Такое волновое число по определению
соответствует волне Нтп в круглом волноводе. Заметим, что числа xm1, xm2, ... и yт1, yт2, ... образуют возрастающие последовательности,
в которых наибольший интерес представляют числа xm1 и yт1,
соответствующие наименьшим значениям ![]() и, следовательно,
наибольшим значениям критических длин волн
и, следовательно,
наибольшим значениям критических длин волн ![]() .
Приведем таблицу значений
.
Приведем таблицу значений ![]() для наиболее важных
волн в круглом волноводе.
для наиболее важных
волн в круглом волноводе.
Таблица 1
|
Волна |
E01 |
E11 |
E21 |
H01 |
H11 |
H21 |
|
|
1,31 |
0,82 |
0,61 |
0,82 |
1,71 |
1,05 |
Из табл. 1 видно, что наибольшее значение ![]() соответствует магнитной волне H11: для нее критическая длина волны равна
1,71 диаметра волновода. Функция
соответствует магнитной волне H11: для нее критическая длина волны равна
1,71 диаметра волновода. Функция ![]() волны H11 определяется формулой
волны H11 определяется формулой
![]() ,
, ![]() ,
, ![]() = l,841,
= l,841,
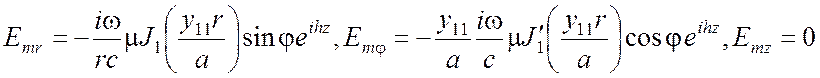 ,
(3.42)
,
(3.42)
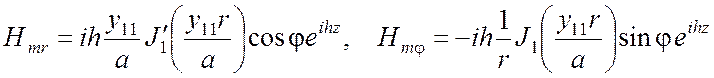 ,
, 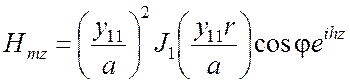
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.