Структура поля волны Нsп
(![]() ) связана со структурой волны Н11
таким же образом, как структура поля волны Еsп связана со структурой волны Е11 (см.
выше).
) связана со структурой волны Н11
таким же образом, как структура поля волны Еsп связана со структурой волны Е11 (см.
выше).
 |
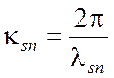 . Волна Н10 имеет наименьшее
значение
. Волна Н10 имеет наименьшее
значение 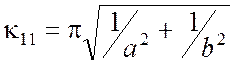 и
и 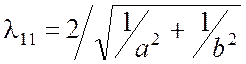
При условии ![]() , имеем
, имеем
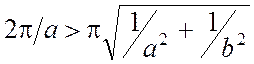 ,
,
поэтому волна Н20 и все другие волны в
прямоугольном волноводе, имеющие более высокие индексы s и п, чем рассмотренные выше четыре волны,
обладают большими значениями ![]() и,
следовательно, более короткими критическими длинами волн
и,
следовательно, более короткими критическими длинами волн ![]() . При
. При
![]() вслед за волнами Н10 и Н01
непосредственно следует волна Н20. При а = 2b критические частоты волн Н01
и Н20 совпадают.
вслед за волнами Н10 и Н01
непосредственно следует волна Н20. При а = 2b критические частоты волн Н01
и Н20 совпадают.
Как было показано ранее, при
длине волны, превышающей критическую, распространение в волноводе невозможно.
Поэтому при условии ![]() > 2а все волны в
прямоугольном волноводе (как электрические, так и магнитные) являются
затухающими волнами, и волновод не может служить линией передачи в этом
диапазоне. При уменьшении волны, когда
> 2а все волны в
прямоугольном волноводе (как электрические, так и магнитные) являются
затухающими волнами, и волновод не может служить линией передачи в этом
диапазоне. При уменьшении волны, когда ![]() становится
меньше 2а, магнитная волна Н10 становится
распространяющейся, и с ее помощью можно передавать электромагнитную энергию
по волноводу. Таким образом, можно говорить о наличии диапазона одноволновости.
При дальнейшем уменьшении длины волны может также распространяться и волна Н01:
так будет при
становится
меньше 2а, магнитная волна Н10 становится
распространяющейся, и с ее помощью можно передавать электромагнитную энергию
по волноводу. Таким образом, можно говорить о наличии диапазона одноволновости.
При дальнейшем уменьшении длины волны может также распространяться и волна Н01:
так будет при ![]() < 2b;
в квадратном волноводе (а = b) критические
значения волн Н10 и Н01 совпадают. Для
более коротких волн число распространяющихся волн становится еще больше, в
частности появляются распространяющиеся волны Е11 и Н11.
Как правило, передача электромагнитной энергии по волноводам с помощью
нескольких распространяющихся волн представляет значительные технические
неудобства, поэтому для заданного диапазона частот размеры прямоугольного
волновода обычно подбираются таким образом, чтобы в нем распространялась только волна Н10, а все
остальные волны были затухающими.
< 2b;
в квадратном волноводе (а = b) критические
значения волн Н10 и Н01 совпадают. Для
более коротких волн число распространяющихся волн становится еще больше, в
частности появляются распространяющиеся волны Е11 и Н11.
Как правило, передача электромагнитной энергии по волноводам с помощью
нескольких распространяющихся волн представляет значительные технические
неудобства, поэтому для заданного диапазона частот размеры прямоугольного
волновода обычно подбираются таким образом, чтобы в нем распространялась только волна Н10, а все
остальные волны были затухающими.
В заключение остановимся на вопросе вырождения волн в прямоугольном волноводе. В граничных задачах бывают случаи, когда две или больше собственных функций соответствуют одному и тому же собственному значению. Это явление называется вырождением, а такие собственные значения называются вырожденными (кратными).
С такими случаями мы встречаемся
в граничной задаче для электрических волн - при решении уравнения (3.7) с
условием (3.11), или в граничной задаче для магнитных волн — при решении
уравнения (3.7) с условием (3.17). Если будем для собственных значений этих
задач писать последовательности ![]() , … ,
, … , ![]() , … и приписывать каждому собственному
значению одну собственную функцию, то при вырождении эти последовательности
будут иметь одинаковые элементы. В прямоугольном волноводе с соизмеримыми
сторонами а и b (т.
е. когда отношение a : b является рациональным числом) всегда будет вырождение.
В частности, в квадратном волноводе, при а = b,
волны Еsп и Еns
, … и приписывать каждому собственному
значению одну собственную функцию, то при вырождении эти последовательности
будут иметь одинаковые элементы. В прямоугольном волноводе с соизмеримыми
сторонами а и b (т.
е. когда отношение a : b является рациональным числом) всегда будет вырождение.
В частности, в квадратном волноводе, при а = b,
волны Еsп и Еns ![]() будут
иметь одинаковые собственные значения, хотя распределения их полей в
пространстве не совпадают
будут
иметь одинаковые собственные значения, хотя распределения их полей в
пространстве не совпадают
Если рассматривать задачу об
электромагнитных волнах в волноводе как одну граничную задачу, то для
прямоугольного волновода характерно особое вырождение, которое можно назвать
вырождением Е - H. Оно заключается в том,
что поперечные волновые числа для волн Еsп
и Нsп совпадают и, таким
образом, вырожденными. Невырожденные собственные значения могут иметь лишь
волны Нт0 и Нтn,
так как электрические волны с теми же индексами не существуют. В
частности, при а > b собственное
значение 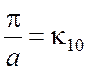 для волны H10
является всегда невырожденным.
для волны H10
является всегда невырожденным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.