Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 30

Собственные волны любой линии передачи обладают весьма важным свойством ортогональности, которое легче всего вывести из леммы Лоренца в ее общей формулировке (6.5). Для этого возьмем в качестве поля  поле какой-нибудь волны с индексом s, а в качестве поля  - поле другой волны с индексом s'. Эти поля не имеют источников, поэтому

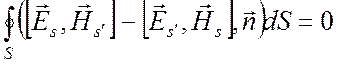.                           (6.26)

Если взять поверхность S в виде двух поперечных сечений волно­вода S₁ и S₂ и заключенной между ними части поверхности S₀ (рис. 6.3), то интеграл по S₀ обращается в нуль согласно усло­виям (6.22), (6.23) или (6.24), наложенных на поля обеих волн с индексами s и s'. В самом деле,

,

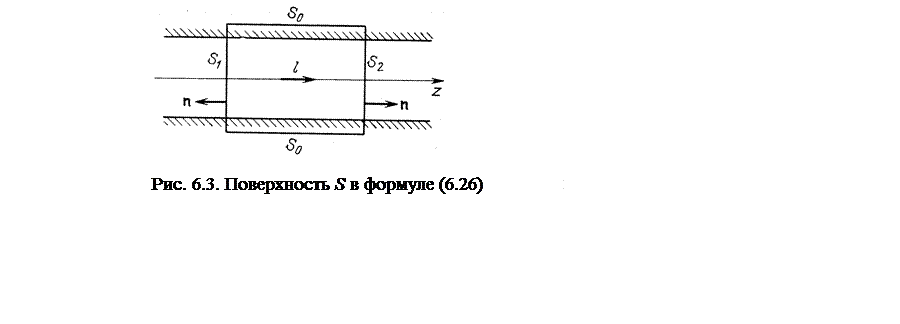
так что при граничном условии (6.22) подынтегральная функция в формуле (6.26) обращается в нуль на S₀. То же будет и при граничном условии (6.23), поскольку

При граничном условии (6.24) подынтегральная функция (6.26) также равна нулю на поверхности S₀.

На поверхности S₂ имеем  = , а на поверхности S₁ вектор  направлен в противоположную сторону и  = - ; напомним, что через  обозна­чен единичный вектор в направлении оси z. Поэтому соотношение (6.26) приводит к выводу, что интеграл

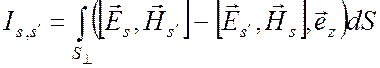,                               (6.27)

взятый по любому поперечному сечению  (при  z = const),   не зависит от z, так как этот интеграл для любых двух сечений S₁ и S₂ имеет одно и то же значение.

Однако поле  пропорционально , а поле  про­порционально . Поэтому

,                              (6.28)

откуда вытекает, что либо  = 0, либо .

При отсутствии вырождения, когда каждому волновому числу h_s соответствует только одна волна, условие  может иметь место только при s' = - s. Поэтому получается соотношение

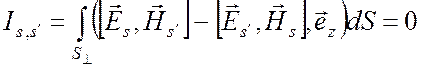 при s' = - s,                 (6.29)

которое является условием ортогональности собственных волн. Если есть вырождение, то кратные волны с одним и тем же волновым числом всегда могут быть подвергнуты дополнительной ортогонализации в смысле соотношения (6.29). Поэтому можно считать, что условие ортогональности (6.29), являющееся основой всего дальнейшего изложения, выполняется для всех волн волноводной системы.

Нормой s - й собственной волны будем называть величину

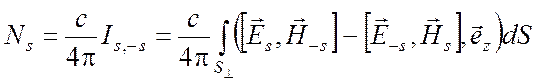.                (6.30)

Норма имеет размерность мощности и в ряде случаев лишь простым численным множителем от комплексной мощности, переносимой s - й волной через поперечное сечение z = 0. Рассмотрим физический смысл полученных формул. Начнем с условия ортогональности (6.29). Если возьмем две волны с та­кими индексами s и s', что s'  s и s' - s, т. е. |s'|  |s|, то мо­жем написать для них два соотношения ортогональности:

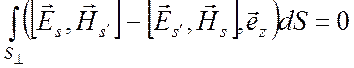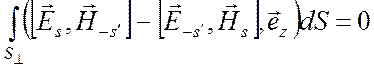, .    (6.31)

Поля прямой электрической волны (индекс s) и встречной электрической волны (индекс - s) связаны соотношениями

, ,  ,          (6.32)

которые легко вывести из уравнений для ТМ поля в волноводе (3.9), (3.10).

,                          .

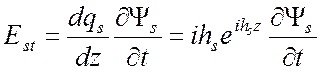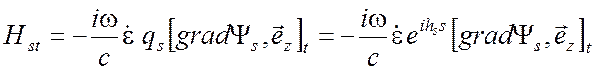Здесь индекс t обозначает касательную проекцию, а * помечено комплексное сопряжение. Воспользовавшись принципом перестановочной двойственности (см.  § 1.5) из формул (6.31) получаем для ТЕ поля следующие соотношения

, ,  , ,        (6.33)

Или, объединив (6.32), (6.33),  можно записать

, ,  , ,       (6.34)

где верхний знак относится к полю ТМ, а нижний – к полю ТЕ.

Пользуясь соотношениями (6.34), легко приведем второе со­отношение (6.31) к виду

.

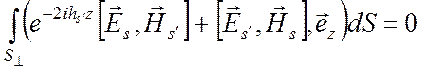Комбинируя  его с первым  соотношением   (6.31),  получаем

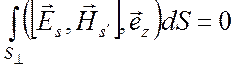 при  |s'|  |s|.                        (6.35)

Физический смысл формулы (6.35) станет ясным, если вычис­лить колеблющуюся мощность, переносимую через поперечное се­чение волновода  полем

,    ,                         (6.36)

т.е., суперпозицией (суммой) волн, распространяющихся в волно­воде в положительном направлении оси z. Рассмотрим сначала интеграл , соответствующий мощности, переносимой отдельной s - волной

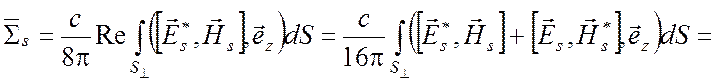
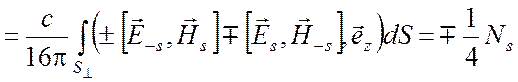,                (6.37)

Видим, что норма отличается лишь множителем  4 от колеблющейся мощности, переносимой s -й волной через поперечное се­чение .