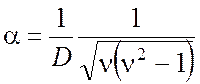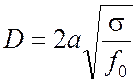Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 22

, .                            (4.40)

Кривая В на рис. 4.1 вычислена по этой формуле.

Заметим, что уникальное свойство волны Н₀₁, а также всех волн Н_0n - убывание их коэффициента затухания с ростом частоты – обусловлено отсутствием у нее продоль­ных токов. Эти волны допускают также точный рас­чет, хотя практически достаточно пользоваться пер­вым приближением метода теории возмущений. Сравнительная простота точного расчета обусловлена тем, что при конечной проводимости стенок волны Н_0п сохраняют свой магнитный характер, т. е. име­ют составляющую E_z = 0. В общем случае этого уже не будет, а именно волны, являющиеся в идеальном волноводе электрическими, под влияни­ем конечной проводимости стенок становятся слегка магнитными, т. е. приобретают небольшую составляющую H_z. Наоборот, маг­нитные волны становятся слегка электрическими благодаря при­обретению малой составляющей E_z. Поэтому электромагнитная волна в неидеальном волноводе представляется в виде суммы эле­ктрической и магнитной волн, распространяющихся с одним и тем же комплексным волновым числом h.

Другой особенностью волны Н_0n является ее вырождение: в идеальном круглом волноводе то же волновое число h₀ имеет вол­на Е₁₁ (см. § 3.3). Под влиянием конечной проводимости стенок это вырождение снимается, поскольку волны Н_0n и Е₁₁ имеют различное затухание.

Однако расщепление волновых чисел h у волн Н_0п и Е₁₁, выз­ванное потерями в стенках, невелико. При более сильных возму­щениях это расщепление не сказывается и волны Н_0п и Е₁₁ свободно трансформируются друг в друга.

Выше предполагалось, что структура поля данной волны слабо изменяется под влиянием конечной проводимости стенок и что данная волна распространяется в неидеальном волноводе как единое целое, не распадаясь на несколько волн. Поэтому получен­ные выше результаты относятся лишь к невырожденным волнам (например, к волне Н₁₀ в прямоугольном волноводе).

Глава 5. Резонаторы

5.1. Постановка задачи о колебаниях в резонаторах

Объемным резонатором называется часть пространства, ог­раниченная металлической стенкой. В таком объеме могут про­исходить электромагнитные колебания, поэтому на сверхвысоких частотах он имеет свойства колебательного контура с высокой до­бротностью. Наряду с термином «объемный резонатор» в том же смысле применяются термины: резонансная полость, резонансный объем, полый резонатор, эндовибратор и т. д.

Предположим, что стенки резонатора обладают идеальной прово­димостью, а пространство внутри резонатора имеет электромаг­нитные свойства пустоты. Рассмотрим обобщенный регулярный волновод, который ограничен двумя идеально проводящими стенками при  z = 0 и z = l.

Для построения решения в объемном резонаторе действуем так же, как и в волноводах, и используем принцип поляризационной двойственности (см. § 1.6). Общее решение ищем в виде суперпозиции фундаментальных решений ТМ и ТЕ типа относительно координаты разделения z. При этом каждое ТМ и ТЕ решение описывается однокомпонентным электрическим (или магнитным) вектором Герца, направленным по координате z:

, ,                                          (5.1)

где  - единичный орт в направлении координаты z. Вектора Герца удовлетворяют дифференциальным уравнениям в частных производных (3.4), для нахождения решения которых пользуемся методом разделения переменных и представлениями

.                                           (5.2)

Тогда, для мембранных функций  получаем уравнения, аналогичные волноводному случаю

,                                                   (5.3)

и для волновых функций q_i(z)

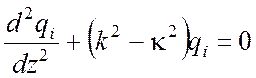,                                               (5.4)

где ,   - поперечное волновое число, h – продольное волновое число.

Компоненты электрического и магнитного полей выражаются через мембранные и волновые функции с помощью соотношений

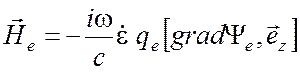,               (5.5)

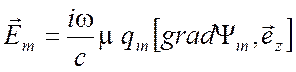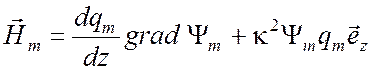,  .           (5.6)

Граничные условия на идеально прово­дящих стенках резонатора заключаются в равенстве нулю тангенциальных составляющих электрического поля, что приводит к условиям для мембранных функций  (3.11) и (3.17):