Индексы s, n и p определяют направления распространения плоских волн, на которые разлагается поле собственных колебаний полости. Двукратное вырождение собственных частот, о котором мы говорили выше, физически связано с тем, что при данном направлении распространения плоской волны ее поляризация может быть произвольной. При сложении плоских волн с одной поляризацией получается первое собственное колебание, при сложении волн с другой, перпендикулярной поляризацией приходим ко второму собственному колебанию, имеющему ту же частоту.
Собственные колебания, у которых один из индексов равен нулю, занимают особое положение. Так, например, тройке чисел 1, 1 и 0 соответствует электромагнитное поле волны Е110
![]() ,
(5.22)
,
(5.22)
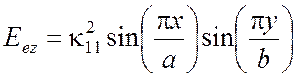 ,
, 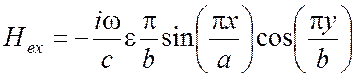 ,
,
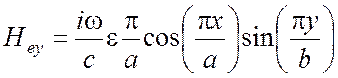 ,
,
где ![]() . Если в нуль
обращаются два индекса, то поле тождественно равно нулю и такие тройки индексов
собственных колебаний не дают.
. Если в нуль
обращаются два индекса, то поле тождественно равно нулю и такие тройки индексов
собственных колебаний не дают.
Электромагнитное поле (5.22) колеблется с собственной частотой
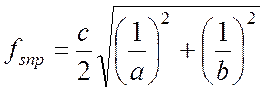 (5.23)
(5.23)
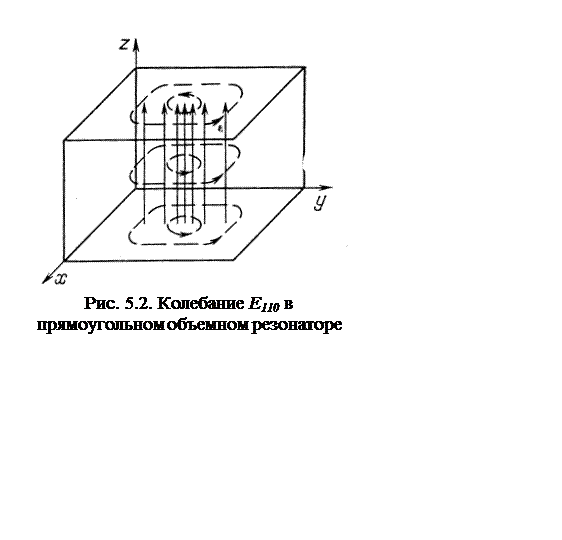 Эта частота может быть невырожденной, поскольку тройке чисел 1, 1, 0
соответствует лишь одно собственное колебание (5.22). Если выполняются условия
а > 1, b >
1, то эта частота будет наименьшей среди всех частот (5.20), притом
невырожденной.
Эта частота может быть невырожденной, поскольку тройке чисел 1, 1, 0
соответствует лишь одно собственное колебание (5.22). Если выполняются условия
а > 1, b >
1, то эта частота будет наименьшей среди всех частот (5.20), притом
невырожденной.
Колебание резонатора называется основным колебанием, если оно имеет наименьшую собственную частоту. Колебание 110 является (при условиях а > 1, b > 1) основным колебанием прямоугольного резонатора и широко применяется на практике.
Структура электромагнитного поля этого колебания изображена на рис. 5.2: электрические силовые линии образуют пучок прямых, параллельных оси z, наиболее густой при х = а/2, у = b/2, а магнитные силовые линии охватывают этот пучок замкнутыми кольцами неправильной формы. Легко показать, что форма магнитных силовых линий та же, что у волны Е11 в прямоугольном волноводе (см. рис.3.2).
В заключение отметим следующую
особенность формул (5.17):в выражения для магнитного поля входит
множитель ±i, отсутствующий у электрического
поля. Это значит, что магнитное поле находится в квадратуре с электрическим, т.
е. сдвинуто по фазе на ![]() /2. Возвращаясь от комплексных
амплитуд к мгновенным значениям полей с помощью формул (1.15), видим, что в некоторый момент времени t электрическое поле исчезает во всем объеме резонатора, а
магнитное поле при этом принимает максимальные значения (по абсолютной
величине); через четверть периода исчезает магнитное поле, а электрическое
достигает максимума и т. д. Таким образом, при собственных колебаниях
электромагнитная энергия дважды за период является чисто электрической и дважды
чисто магнитной, причем происходит непрерывный переход энергии из электрической
формы в магнитную и наоборот. Те же энергетические процессы происходят при
свободных колебаниях обычных резонансных контуров L,
С, а также других объемных резонаторов без потерь.
/2. Возвращаясь от комплексных
амплитуд к мгновенным значениям полей с помощью формул (1.15), видим, что в некоторый момент времени t электрическое поле исчезает во всем объеме резонатора, а
магнитное поле при этом принимает максимальные значения (по абсолютной
величине); через четверть периода исчезает магнитное поле, а электрическое
достигает максимума и т. д. Таким образом, при собственных колебаниях
электромагнитная энергия дважды за период является чисто электрической и дважды
чисто магнитной, причем происходит непрерывный переход энергии из электрической
формы в магнитную и наоборот. Те же энергетические процессы происходят при
свободных колебаниях обычных резонансных контуров L,
С, а также других объемных резонаторов без потерь.
Вычислим среднюю за период энергию электромагнитного поля по формуле (1.22)
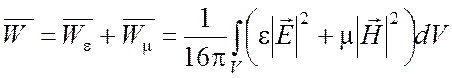 .
.
Тогда электрическая энергия равна
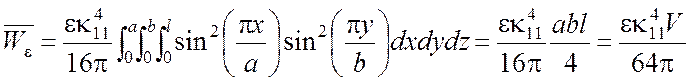 . (5.24)
. (5.24)
Магнитная
энергия вычисляется аналогичным образом и, с учетом того, что справедлива
формула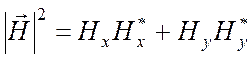 , приходим к выражению
, приходим к выражению
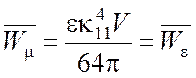 . (5.25)
. (5.25)
Можно показать, что этот результат справедлив для всех типов волн.
Цилиндрическим резонатором называется отрезок круглого волновода, ограниченный двумя металлическими поперечными стенками z = const. (рис. 5.3). Для построения электромагнитного поля в таком резонаторе воспользуемся развитой выше теорией, а также выражениями для мембранных функций, полученных для круглого волновода (см. § 3.3)

![]() ,
, ![]() , s
= 0, 1, …,
, s
= 0, 1, …,
n = 1, 2, …,
![]() ,
,
![]() , (5.26)
, (5.26)
где ![]() - функция Бесселя порядка s,
- функция Бесселя порядка s, ![]() - нули функции Бесселя,
- нули функции Бесселя,
![]() - нули производной
- нули производной ![]() .
.
Тогда для поперечно магнитного поля ТМ получаем выражения:
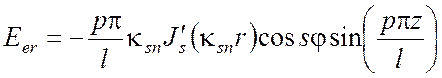 ,
, 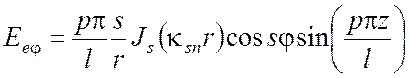 ,
,
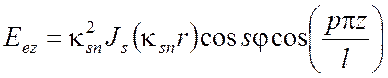 ,
(5.27)
,
(5.27)
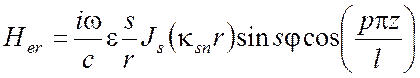 ,
, 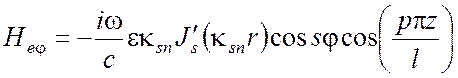 ,
,
![]() ,
,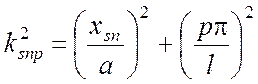 (5.28)
(5.28)
Для поперечно электрического поля ТЕ:
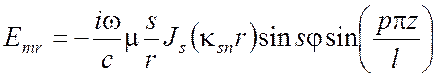 ,
, 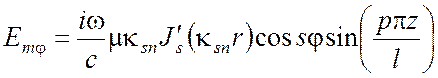 ,
,
![]() ,
,
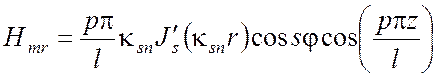 , (5.29)
, (5.29)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.