Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 41

                                        (П2.5)

Поэтому при целых  нужно знать другое решение, линейно независимое от . Одним из таких решений может быть так называемая функция Неймана , или цилиндрическая функция второго рода, определяемая соотношением

                              (П2.6)

Можно показать, что в пределе, когда  стремится к целому значению, функция  остается линейно независимой от . Представления функций Неймана в виде ряда можно найти в математических справочниках [3, 4, 5, 6].

В качестве решений уравнения Бесселя используют также цилиндрические функции третьего рода, или функции Ханкеля, которые определяются линейными комбинациями функций Бесселя и Неймана:

                             (П2.7)

Здесь  и  - функции Ханкеля первого и второго рода порядка .

Цилиндрические функции первого, второго и третьего родов линейно – независимы, так что общее решение уравнения Бесселя можно представить в виде линейной комбинации с произвольными коэффициентами любых из названных функций.

Отметим некоторые свойства цилиндрических функций:

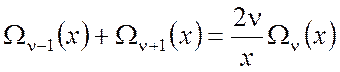                                (П2.8)

,                              (П2.9)

где  - полная производная цилиндрической функции по аргументу, и как следствие:

                                      (П2.10)

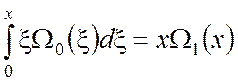                                 (П2.11)

Здесь в качестве цилиндрической функции  может быть взята любая из функций , ,  и .

Приближенные выражения цилиндрических функций при малых значениях аргумента :

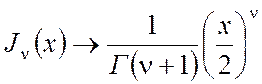,                                (П2.12)

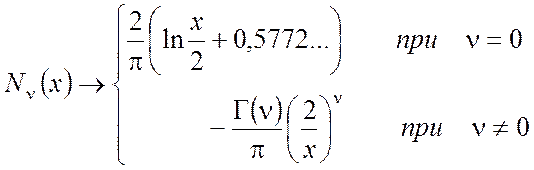                   (П2.13)

Здесь  считается действительным и неотрицательным.

При

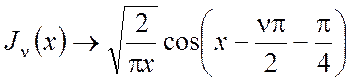                           (П2.14)

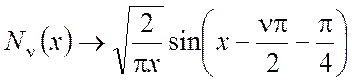                            (П2.15)

Соответствующие выражения для функций Ханкеля могут быть получены из формулы (П2.7)  при помощи соотношений (П2.12), (П2.13) или (П2.14), (П2.16).

Из асимптотического разложения (3.18) видно, что функция Бесселя имеет бесконечное количество корней

                                      (П2.16)

Здесь через  обозначен n-ый корень функции . В таблице приведены значения первых трех корней функций Бесселя :

n	m = 0	m = 1	m = 2
1	2,405	3,832	5,135
2	5,520	7,016	8,417
3	8,654	10,173	11,620

Для больших n корни функции  можно найти по асимптотической формуле .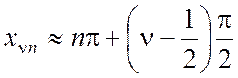 

Можно показать, что система функций Бесселя  с фиксированным  и n = 1, 2, … представляет собой ортогональную систему на интервале . Предполагая, что система функций Бесселя является полной, можно разложить произвольную функцию от r на интервале  в ряд Фурье – Бесселя

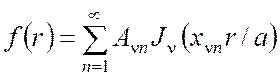,                       (П2.17)

где 

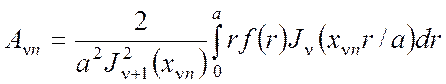                                                 (П2.18)

Разложение (П2.17), (П2.18) особенно удобно для функций, обращающихся в нуль при r = a, т.е. удовлетворяющих однородным условиям.

Литература

1.  Курс лекций В.А. Павлова «Электродинамика»

2.  Вайнштейн Л.А. Электромагнитные волны. М., Радио и связь, 1988.

3.  Бейтмен Г., Эрдейи А. Высшие трансцендентные функции, в трех томах. Т.2. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены.  СМБ, «Наука», 1968.

4.  Градштейн И.С., Рыжик И.М. Таблицы Интегралов, сумм, рядов и произведений. М. Физматгиз, 1962.

5.  Лебедев Н.Н. Специальные функции и их приложения. Физматгиз, 1963.

6.  Янке Е., Эмде Ф., Леш Ф. Специальные функции (формулы, графики, таблицы). М. Наука, 1968.

7.  Григорьев А.Д. Электродинамика и техника СВЧ. М.: Высш. шк., 1990 – 335с.

8.  Михалевский В.С. Элементы теории сверхвысокочастотных замедляющих систем. Изд-во Ростовского ун-та, 1964 – 190с.