Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 16

,                                (3.60)

где - комплексная огибающая начального сигнала, опре­деляемая интегралом

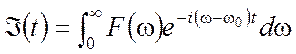                            (3.61)

и являющаяся медленно изменяющейся функцией времени t (по сравнению с ). Медленное изменение  следует из того, что интеграл (3.61) фактически определен (рис. 3.10) в окрестности частоты ; если 2 - ширина частотной полосы, занятой сигналом (), то в интеграле (3.61)  и изменяется не быстрее, чем , и значитель­но медленнее, чем .

При амплитудной модуляции изменяется абсолютная величина , которую обычно называют амплитудой или огибающей сиг­нала. При частотной или фазовой модуляции изменяется фаза комплексной функции . Во всех случаях информацию перено­сит комплексная огибающая . Аппроксимируя функцию  выражением (3.59), получаем функцию f (z, t) в виде

 ,                            (3.62)

где

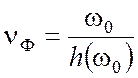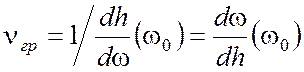,      .                 (3.63)

Таким образом, комплексная огибающая и высокочастотное за­полнение перемещаются с разными скоростями. Заполнение пере­мещается с фазовой скоростью введенной выше формулой (3.55), в которой надо заменить  на . Комплексная огибаю­щая движется с групповой скоростью :с этой скоростью переда­ется энергия сигнала, пропорциональная ||², и связанная с ним информация.

Термин «групповая скорость» объясняется тем, что рассмат­риваемый сигнал (3.57) с узким спектром частот называется группой волн или квазимонохроматической группой; последнее на­звание подчеркивает узость спектрального состава. Групповую скорость можно назвать просто скоростью сигнала, поскольку вся информация передается комплексной огибающей, а не высокочас­тотным заполнением.

Заметим, что в механике скорость материальной точки опре­деляется единственным образом, а при анализе волновых процес­сов приходится вводить фазовую и групповую скорости. Это объясняется тем, что от­дельные монохроматические волны, входящие в состав сигналов, распространяются в общем случае с различными фазовыми ско­ростями, и вследствие этого форма сигнала при его распростра­нении искажается. По этой причине получаем различные значения скоростей в зависимости от того, за каким признаком сигнала следим при его перемещении.

Зависимость фазовой скорости (3.55) от частоты называется дисперсией. Постоянство фазовой скорости - это отсутствие дис­персии, тогда отношение 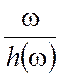 постоянно и справедливо выра­жение (3.58), согласно которому групповая скорость равна фа­зовой. Справедливо и обратное, равенство этих скоростей при всех частотах при­водит к их независимости от частоты.

Отметим, что при наличии дисперсии групповая скорость лишь приближенно характеризует распространение сигнала. Дело в том, что к понятию групповой скорости и формуле (3.62) приходим, заменяя  линейной функцией (3.59). Если произвести уточ­нение, учесть следующие члены ряда Тейлора, то окажется, что при достаточно больших z приближенное выражение (3.62) зна­чительно отличается от точного выражения (3.57). Это происхо­дит потому, что малые поправки к формуле (3.59) умножаются в интеграле (3.57) на z.

Поэтому на очень больших расстояниях его огибающая уже не перемещается со скоростью как единое целое, а происходит деформация сигнала. Чем уже спектральный диапазон сигнала, тем деформация происходит медленнее, так как с тем большей точностью применимо выражение (3.59).

Рассмотрим распространение модулированных волн в волноводе. Волновое число  распространяющейся  волны  в  волноводе

                                (3.64)

где , а от частоты не зависит. Ее фазовая скорость

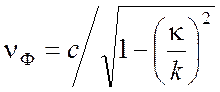.                                    (3.65)

Она характеризует скорость распространения фазы в монохрома­тической волне, являющейся в пространстве (вдоль оси z)и во времени бесконечной синусоидой.

Фазовая скорость в волноводе по формуле (3.65) превосхо­дит с. Этот результат не противоречит теории относительности, запрещающей передачу сигналов и движение тел со скоростью, превышающей скорость света. Как отмечалось ранее, с помощью монохроматической волны нельзя передавать сигнал, несущий ка­кую-либо информацию. Передача информации возможна лишь с помощью модулированных волн, не являющихся монохроматичес­кими, причем информацию и энергию несет комплексная огибаю­щая, перемещение которой происходит с так называемой группо­вой скоростью