Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 37

Получим уравнение для функции . Для этого перепишем (7.14) следующим образом

.                                (7.18)

Учитывая, что

,                                   

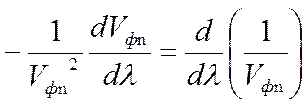получим искомое уравнение

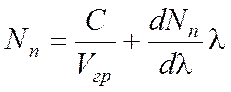.                                    (7.19)

Из этого уравнения следует, что если мы выберем длину волны внутри полосы пропускания и проведем касательную к дисперсионной характеристике

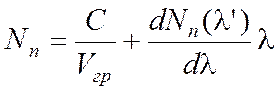,                                (7.20)

то она отсечет на оси ординат отрезок, равный . Из этого следует, что для фиксированной частоты касательные к дисперсионным характеристикам всех пространственных гармоник пересекаются в одной точке (т.к. все пространственные гармоники имеют одну и ту же групповую скорость). Причем касательные не могут пересекать ось ординат на отрезке 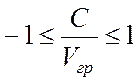, т.к.  .           

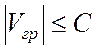На рис. 7.4 приведены дисперсионные характеристики  ЗС для двух разных случаев – возрастания  от 0 до при изменении длины волны от  до  (сплошная линия) и убывания от  до 0 (пунктирная линия).

Рис. 7.4

Приведем классификацию дисперсионных характеристик ЗС. Каждая ЗС имеет бесконечное число волн, распространяющихся в одну и другую сторону вдоль нее, однако групповая скорость имеет строго определенное направление, которое примем за положительное направление. Дисперсию пространственной гармоники называют положительной, если групповая и фазовая скорости сонаправлены и отрицательной, если их направления противоположны. Кроме того, по аналогии с оптикой различают нормальную 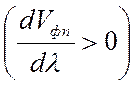  и аномальную  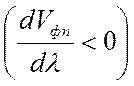дисперсии, причем сама фазовая скорость может быть как положительной, так и отрицательной. Таким образом, возможны следующие типы дисперсии волн в ЗС: положительная нормальная, положительная аномальная и отрицательная нормальная. Отрицательная аномальная дисперсия невозможна, т.к. групповая скорость ограничена скоростью света. Рассмотрим свойства волн с различным типом дисперсии, основываясь на выражении (7.18).

1.  Положительная нормальная дисперсия  :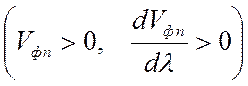

·  фазовая скорость всегда больше групповой ,

·  минимальное значение крутизны дисперсионной  характеристики 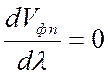 достигается для медленных волн, при этом .

·  на границах полосы пропускания, где , .

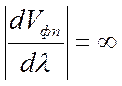2.  Положительная аномальная дисперсия  :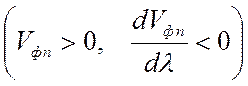

·  фазовая скорость меньше групповой ,

·  крутизна дисперсионной характеристики может достигать значения 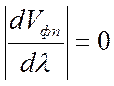, при этом .

·  групповая скорость не обращается в нуль. Следовательно, аномальная положительная дисперсия может существовать только в части полосы пропускания. Вблизи границ полосы пропускания тип дисперсии меняется на положительную нормальную.

3.  Отрицательная нормальная дисперсия  :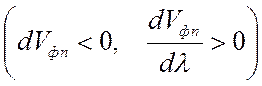

·  минимальная крутизна дисперсионной характеристики равна 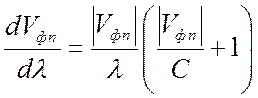, при этом .

7.3. Распределение СВЧ поля в ЗС

Рассмотрим вопрос о распределении СВЧ поля в замедляющих системах. Пространственные гармоники удовлетворяют волновому уравнению. Запишем его для напряженности электрического поля

.                                 (7.21)

Подставим в это уравнение выражение для поля в виде ряда пространственных гармоник

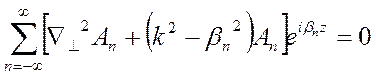.                   (7.22)

Умножив (7.22) на 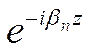 и проинтегрировав по  по периоду, получим уравнение для пространственных гармоник

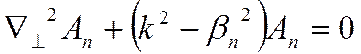..                              (7.23)

Запишем это уравнение для медленных волн в декартовой системе координат

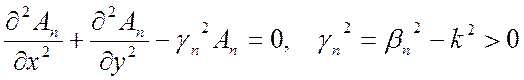 .                  (7.24)

Предположим, что поле не зависит от одной из поперечных координат 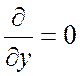. Это справедливо, например, для ЗС типа плоской гребенки. Тогда решение будет иметь вид

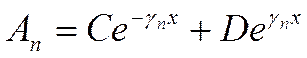.                             (7.25)

Для открытых ЗС . Таким образом, поле носит поверхностный характер. Оно экспоненциально затухает по мере удаления от поверхности ЗС, причем это затухание тем сильнее, чем больше номер пространственной гармоники. Последнее следует из соотношения .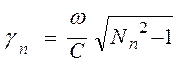

Те же результаты можно получить и для ЗС спирального типа. Для этого запишем уравнение (7.23) в цилиндрической системе координат