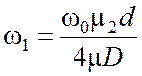Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 26

                                         (5.38)

Таким образом, получаем, что коэффициент затухания пропорционален глубине скин - слоя d и обратно пропорционален корню из проводимости 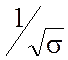; пропорционален корню из резонансной частоты  (глубина скин - слоя  ).

Рассмотрим физический смысл величины D. Для этого введем понятие добротности контура Q как отношение средней энергии к потерям за период T и,  используя формулу (5.32), получаем

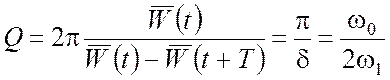,                                (5.39)

где  - логарифмический декремент затухания.

Сопоставив формулы (5.38) и (5.39), находим

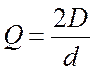                                                   (5.40)

Оценим величину D, имеющую размерность длины. Воспользуемся формулой (5.37). Для грубой оценки заменим в числителе  и  знаменателе этой формулы 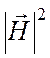  и  некоторым средним значением квадрата магнитного поля, тогда , где V - объем резонатора,  S - его поверхность.  Если все размеры объемного резонатора имеют один и тот же порядок величины, то тот же порядок имеет и D. В этом случае добротность (5.4) по порядку величины имеет равна размеру резонатора, деленному на глубину скин – слоя. Если резонатор имеет вид цилиндра с малой высотой l, то V ~ Sl, и D ~ l, поэтому D имеет порядок меньшего размера резонатора. Такие цилиндрические резонаторы имеют пониженную добротность.

Глава 6. Возбуждение электромагнитных волн

6.1. Лемма Лоренца и теорема взаимности

Лемма Лоренца есть вспомогательное математическое соотношение, связывающее комплексные амплитуды электромагнитных полей, возбуждаемых двумя системами источников. Пусть имеется некоторое пространство, заполненное веществом с комплексными диэлектрическими и магнитными проницаемостями ,  и проводимостью . В общем случае  ,  являются тензорами, что соответствует анизотропному пространству, и зависит от координат (свойство неоднородности).

Пусть поле  возбуждается сторонними токами  и удовлетворяет уравнениям Максвелла

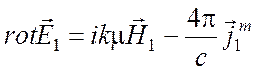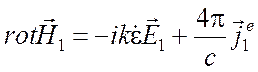,                           (6.1)

а поле  возбуждается сторонними токами  и, сле­довательно, удовлетворяет уравнениям

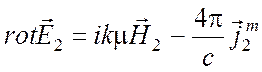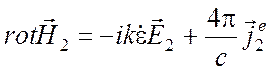,  .                 (6.2)

Оба электромагнитных процесса имеют одну и ту же частоту .

Умножим первое уравнение (6.1) скалярно на , а второе уравнение (6.2) - на  и сложим

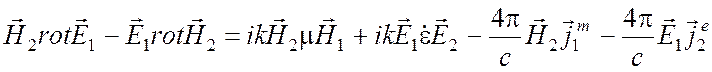
аналогично получаем второе тождество

.

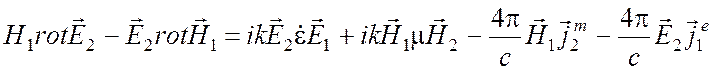Вычитая это тождество из первого и пользуясь известной форму­лой векторного анализа

,

получаем соотношение

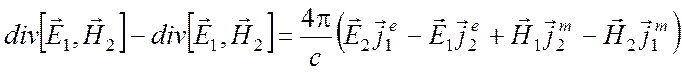,           (6.3)

при выполнении равенств .                  (6.4)

(6.3) представляет собой лемму Лоренца в дифференциальной фор­ме. Интегрируя по произвольному объему V и пользуясь теоремой Гаусса - Остроградского (см. (П1.21) Приложения 1), получаем лемму Лоренца в интегральном виде

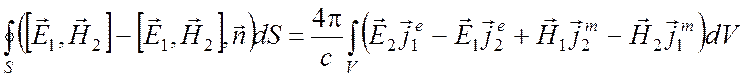,         (6.5)

где S — поверхность, ограничивающая объем V,  - ее внешняя нормаль.

Условия (6.4) выполняются всегда для изотропных сред, когда ,   не являются тензорами, но могут зависеть от координат, а также для частного случая анизотропной среды, когда ,  - симметричные тензоры , .

Частная формулировка леммы Лоренца получается, если в ка­честве объема V возьмем все бесконечное пространство, т. е. бу­дем считать S бесконечно большой сферой. Принимая, как при доказательстве теоремы единственности в § 1.4, что все источни­ки — электрические и магнитные токи — находятся в конечной области пространства, и, считая, что на сфере S выполняются ус­ловия

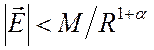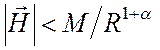, при                        (6.6),

получаем в левой части формулы (6.5) исчезаю­щий интеграл. Поэтому лемма Лоренца для безграничного пространства, имеющего в каждой точке некоторые потери, принимает вид

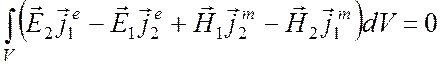.                        (6.7)

В пределе это соотношение справедливо и для пространства без потерь.

Выведенная выше лемма Лоренца имеет многообразные при­менения. Докажем с ее помощью теорему взаимности для элементарных электрических диполей.

Пусть имеются только сторонние электрические токи с плот­ностями  и , а сторонние магнитные токи отсутствуют. Тогда формула (6.7) упрощается следующим образом:

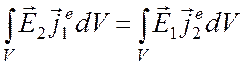.                                   (6.8)