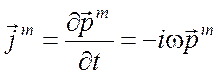Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 28

.                              (6.12)

Используя лемму Лоренца в форме (6.7) и учитывая, что электрические сторонние токи отсутствуют, а интегралы от маг­нитных сторонних токов преобразуются к виду

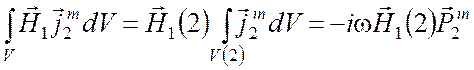
приходим к соотношению

,                                           (6.13)

которое является теоремой взаимности для двух магнитных диполей.

Рассмотрим теорему взаимности  для  двух  диполей различных типов - магнитного диполя  находящегося в точке 1, возбуждающего поле  и электрического диполя , находящегося в точке 2 и возбуждающего поле . Соответствующие плотности тока имеют вид

, .              (6.14)

Подставляя эти выражения в соотношение  (6.7), получаем но­вую теорему взаимности

.                                     (6.15)

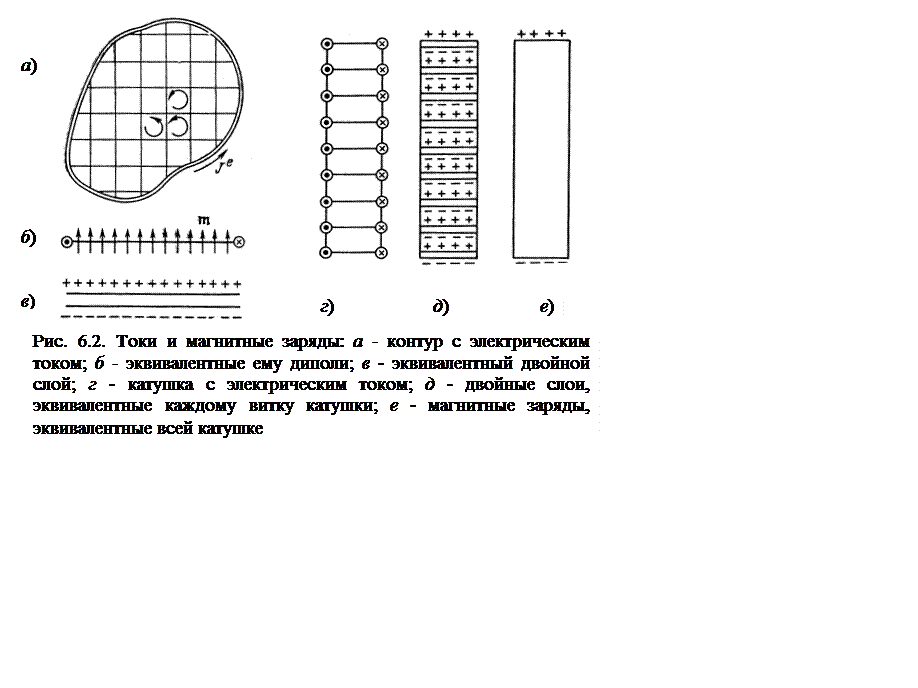
Выведенные в этом параграфе теоремы взаимности имеют  пока формальный характер, поскольку физический смысл понятий магнитный ток и магнитный диполь неясен. Как уже отмеча­юсь ранее, магнитные токи в природе не существуют и вводятся по аналогии с электрическими токами для облегчения математической трактовки полей. Покажем, что если сторонний электрический ток течет по бесконечно малому замкнутому контуру С, то такая система в отношении создаваемого ею электромагнитного поля полностью эк­вивалентна магнитному диполю с моментом

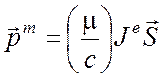,                                     (6.16)

где  - комплексная магнитная проницаемость среды в месте расположения контура С; a  есть векторная площадь, ограничен­ная этим контуром:

.                                      (6.17)

В этой формуле интегрирование производится по любой поверх­ности, натянутой на контур С, а нормаль  связана с направле­нием положительного обхода контура С правилом правого винта. Соотношениями (6.16) и (6.17) широко пользуются в маг­нитостатике, где магнитные диполи и магнитные заряды также вводят чисто формально, заменяя ими реально существующие замкнутые электрические токи. С помощью леммы Лоренца эти соотношения легко обосновать для электродинамических полей. Для этого возьмем в качестве источника поля  сторонний электрический ток , текущий по бесконечно малому контуру С, расположенному в точке 1. Источником поля  по-прежнему будем считать электрический диполь  в точке 2. Применяя к этим двум полям соотношение (6.7), будем иметь

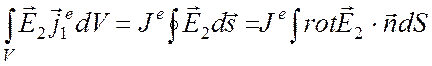                  (6.18)

так как для линейного тока, текущего по контуру С,  где - элемент дуги этого контура. В силу уравнения  выражение (6.18) принимает вид

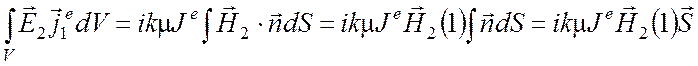
Здесь учтено, что контур С бесконечно мал, благодаря чему маг­нитное поле  и комплексную магнитную проницаемость  мож­но вынести за знак интеграла и воспользоваться формулой (6.17). Остальные интегралы в формуле (6.7) вычисляются без труда, и лемма Лоренца (73.05) приводит к соотношению

.                                (6.19)

Сравним теперь соотношения (6.19) и (6.15), для чего возь­мем поле  и диполь  в обоих случаях одинаковыми. Для того чтобы получить то же самое электрическое поле  в точке 2 в обеих задачах, достаточно взять момент магнитного диполя (6.16). Вектор  и точка 2 могут быть выбраны произвольным образом. Тем самым доказано, что электрическое поле замкнутого электрического тока и элементарного магнитного ди­поля совпадают, если момент магнитного диполя определить фор­мулой (6.16). Из уравнений электромагнитного поля вытекает, что магнитное поле обеих систем также совпадает всюду, за исключением точки, где находится сам диполь или контур с током. Так как конечный замкнутый контур, обтекаемый током , может быть разложен на совокупность элементарных контуров с током, а каждый такой элементарный ток можно заменить элементарным магнитным ди­полем (рис.6.2,б), то окончательно контур с током оказывается эквивалентным двойному магнитному слою или магнитному лист­ку (рис.6.2,в). Катушка (рис.6.2,г), состоящая из многих вит­ков - контуров с постоянным током, может быть заменена пачкой магнитных листков (рис.6.2,д). Поскольку противоположные магнитные заряды на соприкасающихся поверхностях магнит­ах листков взаимно уничтожаются, то такая пачка эквивалентна стержню с магнитными зарядами на концах (рис.6.2,е), т. е. постоянному магниту. Таким путем доказывается эквивалентность кату­шки с током и постоянного магнита, рассматриваемого как совокупность магнитных зарядов. Из магнитостатики известно, что эта эквивалентность имеет место лишь для внешних точек пространства, а внутри магнита напряженность его магнитного поля противоположна напряженности магнитного поля в катушке. Доказанное выше положение вскрывает смысл магнитных токов и магнитных диполей. В частности, соотношение (6.13) можно характеризовать как теорему взаимности для двух рамочных антенн, выполненных в виде малых замкнутых контуров с током. Соотношение (6.15) есть теорема взаимности для  элементарной рамки и элементарного электрического диполя - вибратора Герца.