Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 3

Тогда (1.41) приводится к уравнению для векторного потенциала

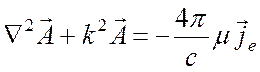                                        .                                (1.43)

Используя уравнение (1.38) и условие калибровки Лоренца, получим уравнение для скалярного потенциала

                                         .                                       (1.44)

Таким образом, источником векторного потенциала  является плотность стороннего тока , а источником скалярного потенциала  - плотность стороннего заряда .

Наряду с векторным потенциалом  и скалярным потенциалом  вводят еще один потенциал — вектор Герца  с помощью соотношений

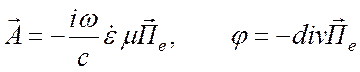,                                (1.45)

причем получаемые по этим формулам потенциалы   и  авто­матически удовлетворяют дополнительному соотношению (1.42).

Если потенциал Герца определен, то электромагнитное поле находится с помощью операции дифференцирования:

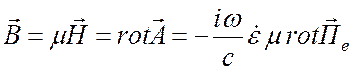                              ,                            (1.47)

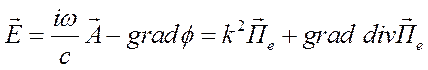
Введенный выше вектор Герца  часто называют электрическим вектором Герца в отличие от магнитного вектора Герца , который вводится следующим образом. Воспользуемся так называемым принципом перестановочной двойственности.

Источниками электромагнитного поля являются сторонние заряды и электрические токи. Известно, что в природе не существуют магнитные заряды и магнитные токи. По этой причине они не входят в уравнения Максвелла. Однако, для удобства решения ряда задач оказывается полезным ввести в уравнения Максвелла фиктивные магнитные источники зарядов  и токов . Такая процедура позволяет использовать полученные ранее решения для построения решений новых задач с помощью простой замены (перестановки) параметров в этих готовых решениях. Запишем уравнения Максвелла с фиктивными магнитными , и реальными электрическими источниками

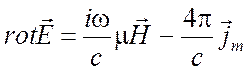                                                                            (1.49)

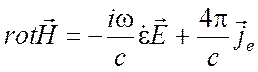                                                                          (1.50)

                              ,                                                      (1.51)

                              ,                                                          (1.52)

                                            (1.53)

Рассмотрим две задачи. Пусть в первой задаче источниками поля  являются электрические заряды и токи, а во второй задаче поле  создается магнитными источниками. Этой ситуации отвечают две системы

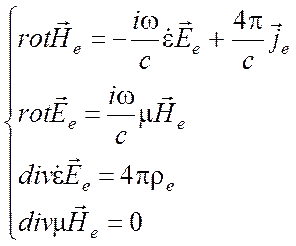
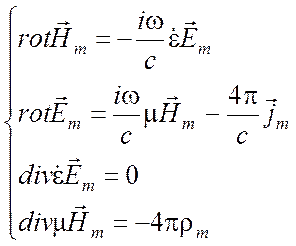                               (1.54)

Эти системы уравнений обладают свойством перестановочной двойственности. Если сделать замену

,                             (1.55)

то полная система уравнений сохраняется. Таким образом, по известному решению первой задачи с помощью простой перестановки находится решение второй задачи.

1.6. Принцип поляризационной двойственности

Для исследования электромагнитного поля при наличии по­верхностей раздела сложной формы часто вместо декартовых ко­ординат х, у, z используются криволинейные координаты , связанные с декартовыми однозначно:

х =  х (), у = y(),  z = z()

На рис. 1.2 изображен бесконечно малый прямоугольный па­раллелепипед (слегка искривленный), образованный тремя коор­динатными поверхностями

=const,  = const,  = const

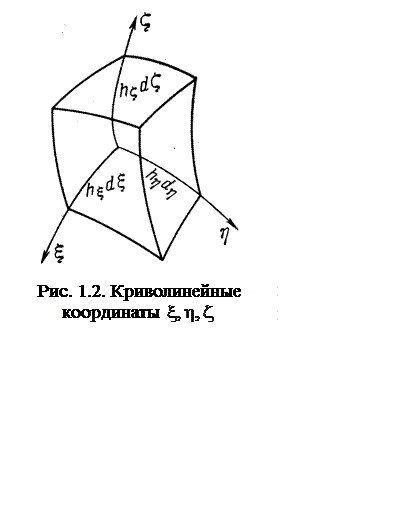и тремя бесконечно близкими поверхностями, соответствующими значениям  + d,  + d,  + d; в дальнейшем считаем дифферен­циалы d, d, dположительными.

В криволинейной системе координат () квадрат элемента длины  и элемент объема  выражаются формулами  и  соответственно, где  - параметры Ламэ.

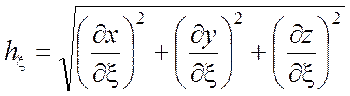                                   (П1.1)

- параметр Ламэ по координате . Параметры Ламэ  и  определяются аналогично (П1.1).

Градиент функции

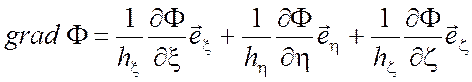,                       (П1.2)

где , , и  - единичные орты в направлении координатных осей  и . Дивергенция вектора

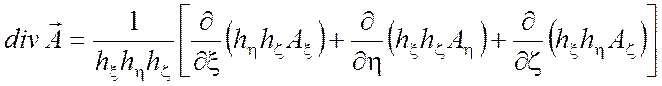           (П1.3)

Ротор вектора

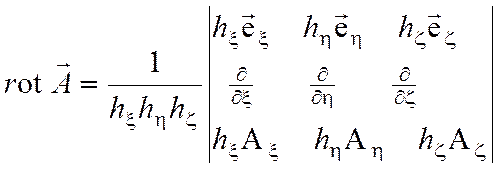                          (П1.4)

Оператор Лапласа (Лапласиан)

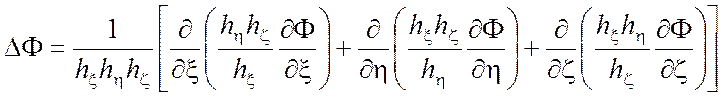      (П1.5)