Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 11

Так как в центре прямо­угольника при  х = а/2 , и у = b/2 функция  принимает максимальное значение, то вблизи него линии уровня имеют вид эллипсов, центры которых совпадают с центром прямоугольника, а полуоси на­правлены по осям х и у и относятся как а: b. По мере увеличения размера эллипса его форма искажается и он начинает все больше походить на прямоугольник со слегка закругленными углами. 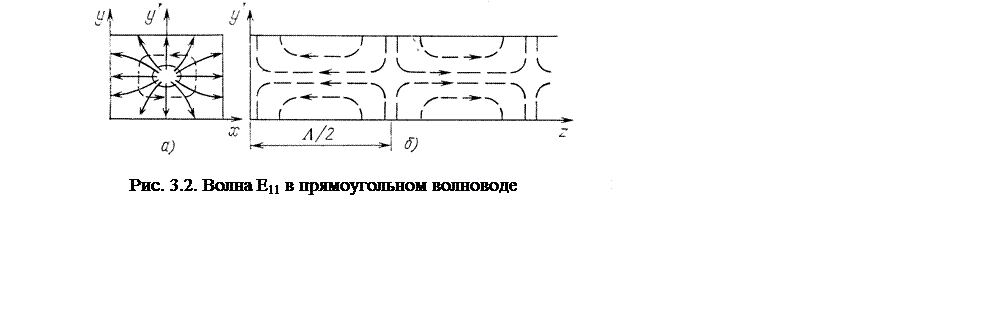На­конец, линия уровня   = 0 есть не что иное, как сам периметр пря­моугольника. Изображенные на рис. 3.2,а  штриховые линии  = const дают сило­вые линии магнитного поля, а перпендикулярные к ним сплошные кривые на рис. 3.2,а дают электрические силовые линии.

Силовые линии электрического поля распространяющейся вол­ны Е₁₁ в продольном сечении у, z  изображены на рис. 3.2,б, из ко­торого видно, что силовые линии начинаются на стенках и идут сначала перпендикулярно этим стенкам — в плоскости поперечно­го сечения. Затем, приближаясь к оси волновода, они отходят от этого сечения, идут в основном параллельно оси волновода и кон­чаются опять на стенке, подходя к ней под прямым углом в плоскости другого поперечного сечения. Картина силовых линий в плоскости продольного сечения обладает периодом, равным длине волны в волноводе .

Структура электромагнитного поля волны Е_sп в прямоуголь­ном волноводе может быть получена следующим образом: если разбить сторону прямоугольника а на s равных частей, а сторо­ну b на п равных частей и через соответствующие точки провести прямые, параллельные осям х и у, то прямоугольное поперечное сечение волновода разобьется на s x п одинаковых прямоуголь­ников. Легко показать, что в каждом малом прямоугольнике элек­тромагнитное поле волны Е_sп имеет ту же структуру, которую имеет в волноводе с таким поперечным сечением рассмотренная выше волна Е₁₁. Поэтому электромагнитное поле волны Е_sп в прямоугольном волноводе является лишь многократным повторе­нием поля волны Е₁₁, но в более мелком масштабе. Доказательст­во этих утверждений легко получается из сравнения формул (3.25) и (3.30).

Перейдем к рассмотрению магнитных волн. С практической точки зрения наиболее важна волна Н₁₀, для которой справедливо

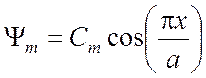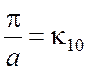,                                  (3.32)

С помощью формул (3.15), (3.16) легко вычислить  составляющие электромагнитного поля волны Н₁₀:

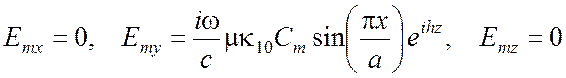                (3.33)

, .

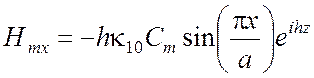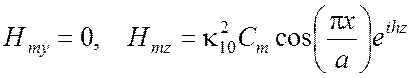Из этих формул видно, что электрическое поле волны Н₁₀ направ­лено по оси у, причем наибольшая густота силовых линий дости­гается при х = а/2. Магнитные силовые линии лежат в горизон­тальных плоскостях, их проекции на плоскости поперечного се­чения являются горизонтальными прямыми, изображенными на рис. 3.3,а  штриховыми линиями. Если изображать силовые линии магнитного поля распространяющейся волны Н₁₀ в плоскости продольного сечения х, z, то это будут замкнутые кривые (рис. 3.3,б).

Структура поля волны Н_s0 является s - кратным повторением структуры волны Н₁₀ по оси х. Структура поля волны Н₀₁ та же, что и у волны Н₁₀, но с заменой оси х на ось у и наоборот. Поле волны Н_0п является n - кратным повторением поля волны Н₀₁  по оси у в уменьшенном масштабе.

Функция  для волны Н₁₁ в прямоугольном волноводе опре­деляется формулой

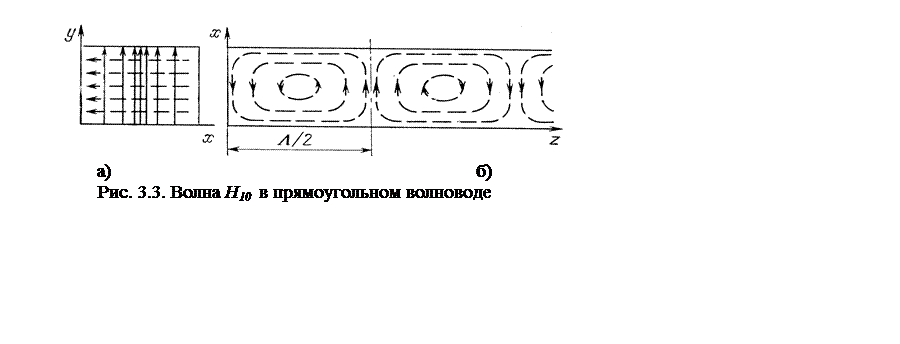
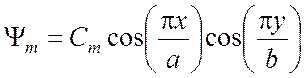.                                     (3.34)

Линии уровня этой функции изображены на рис. 3.4,а. Эту карти­ну легко построить, если учесть, что в каждой вершине прямо­угольника функция (3.34) достигает своего максимального или минимального значения, так что вблизи каждой вершины пря­моугольника линии уровня имеют вид эллипсов (точнее, вблизи каждого угла имеет значение лишь четверть эллипса). При уда­лении от вершины форма эллипсов искажается и они становятся похожими на гиперболы, имеющие в качестве асимптот прямые х = а/2, y = b/2, являющиеся линиями уровня  = 0.

Магнитные силовые линии в плоскости поперечного сечения изображены на рис.3.4,а штриховой линией. Они являются про­странственными кривыми, и их проекции на плоскость продоль­ного сечения у, z для распространяющейся волны Н₁₁ изобра­жены на рис. 3.4,б.