Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 6

Пользуясь соотношениями (1.15), получаем

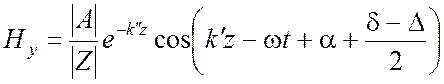,       (2.8)

Эти формулы показывают, что, отвлекаясь от экспоненциаль­ного множителя , мы имеем электромагнитную волну, распро­страняющуюся со скоростью

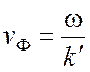,                                                         (2.9)

называемой фазовой скоростью, поскольку составляющие Е_х и Н_у изменяются в зависимости от и t по закону

,  = const.

Распространение благодаря наличию экспоненциального множите­ля  сопровождается затуханием, причем амплитуда поля уменьшается в е раз при прохождении волной расстояния

d=1/k".(2.10)

Расстояние d называется глубиной проникновения поля в данную сре­ду, а для металлических проводников имеет еще одно название - толщина скин - слоя;

Таким образом, физический смысл  заключается в том, что он определяет фазовую скорость распространения волны в данном веществе, поскольку речь идет о фазе плоской монохроматической волны (2.8).

Величина k" определяет затухание волн при распростра­нении в данной среде и связанную с этим затуханием глубину про­никновения d.

2.2. Распространение электромагнитных волн в различных средах

Дадим краткий обзор электродинамических свойств различ­ных сред и зависимости этих свойств от частоты.

Наиболее простыми свойствами обладает пустота, для которой  = 1 и  = 1. Пустота является единственной средой, в которой нет дисперсии (зависимости волнового числа от частоты) и потерь. Так как для нее Z = 1, то плоская распространяющаяся волна (2.7)в пустоте имеет вид

,                              (2.13)

где волновое число 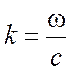  имеет простой физический смысл — оно определяет пространственную зави­симость плоской электромагнитной волны в пустоте. Оно связано длиной волны в пустоте формулой

,                                   (2.14)

где f - частота. Длина волны , как видно из формулы (2.14), есть пространственный период плоской волны в пустоте. Скорость плоских волн в пустоте равна с и не зависит от частоты. Ввиду электромагнитного характера световых волн скорость с кратко на­зывают скоростью света.

В других средах законы распространения плоских волн иные.

Если взять диэлектрики, имеющие в постоянных полях и при низких частотах пренебрежимо малую проводимость, магнитную проницаемость  = 1 и некоторую вещественную диэлектрическую постоянную , то для них

, ,

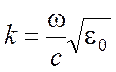Показатель преломления  для диэлектриков равен . Это соотношение между показателем преломления для волн в прозрачном диэлектрике и его диэлектрической постоянной на­зывается соотношением Максвелла. Это соотношение применимо лишь для таких частот, при которых диэлектрическая проница­емость  практически совпадает со статической диэлектрической постоянной . Если же при данной частоте  отличается от , то нужно применять соотношение , справедливое для всех веществ, имеющих  = 1.

Все диэлектрики в той или иной степени имеют дисперсию, и при достаточно высоких частотах для каждого диэлектрика соот­ношение становится неправильным и должно быть заме­нено соотношением . Наиболее ярким примером неприме­нимости соотношения Максвелла к электромагнитным волнам весьма высокой частоты является вода, имеющая при низких ча­стотах  = 81 и n = 1,32 для инфракрасных волн  ( ~ 1мкм).

Вода является примером дипольного (полярного) диэлектрика. Поляризация таких диэлектриков происходит в результате пово­рота молекул, обладающих сильной инерцией, поэтому дисперсия диэлектрической проницаемости проявляется для них в радио­диапазоне. Для воды дисперсия начинается при частотах f ~ 10¹⁰ Гц, что соответствует длине волны  ~ 3 см. Для спиртов, молекулы которых более сложны, дисперсия появляется при еще более низких частотах (f ~ 10⁹ Гц). Как правило, при сильной дисперсии в некотором диапазоне частот в том же диапазоне имеются большие диэлек­трические потери.

Другими свойствами обладают неполярные диэлектрики, на­пример сухой неионизированный воздух, водород, бензол, гелий, неон и другие инертные газы; из твердых веществ — сера и алмаз. Поляризация этих диэлектриков обусловлена смещением электронов внутри атомов и молекул. Для них соотношение Максвелла  выполняется иногда даже в оптическом диапазоне. Объясняется это тем, что электроны обладают малой инерцией и сле­дуют за изменениями поля вплоть до весьма высоких частот.