Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 35

Для значительного замедления электромагнитных волн применяются специальные периодические волноведущие структуры, называемые часто, в силу их широкой распространенности, просто замедляющими системами (ЗС). Существует огромное число типов ЗС (рис. 7.1).

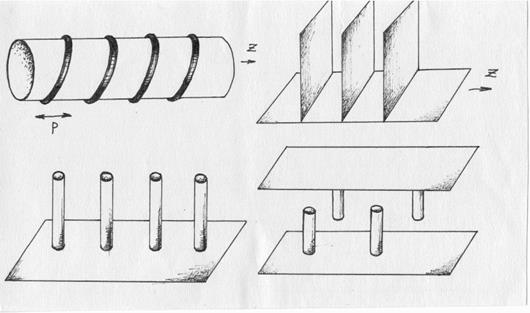
Рис. 7.1

Все они обладают пространственной периодичностью в направлении распространения волн. Прежде чем рассматривать конкретные типы ЗС, выясним их свойства, вытекающие из указанной периодичности и не зависящие от геометрических особенностей ЗС.

На рис. 7.2. представлена произвольная периодическая вдоль оси Z  структура в виде последовательности одинаковых ячеек длины  p.

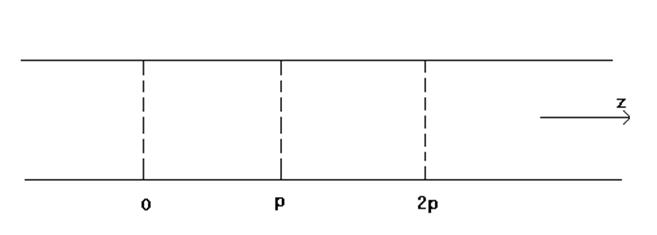
Рис. 7.2

Из периодичности границы рассматриваемой структуры следует, что поля в поперечных сечениях, отстоящих друг от друга на период p могут отличаться только на комплексную константу. Это относится к векторам напряженности электрического и магнитного поля, компонентам вектора Герца и другим функциям, определяющим электромагнитное поле. Данное утверждение носит название теоремы Флоке. Если предположить, что в системе отсутствуют потери, то модуль указанной константы равен единице (при распространении вдоль ЗС сигнал не затухает) и условие теоремы Флоке для напряженности электрического поля можно записать следующим образом

            (7.1)

Входящая в выражение (7.1) величина  зависит от частоты возбужденного в ЗС поля. Ниже мы увидим, что именно зависимость  определяет дисперсионные свойства ЗС. Таким образом, поле в периодической структуре не является периодической функцией (этому «мешает» сомножитель )  Представим поле в следующем виде, выделив в нем периодическую часть:

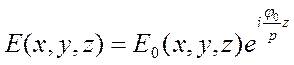        (7.2)

Здесь  – периодическая функция с периодом  p:

.                          (7.3)

При этом условие Флоке будет выполняться, в чем можно убедиться, подставив (7.2) в (7.1) с учетом (7.3).

Разложим функцию  в ряд Фурье

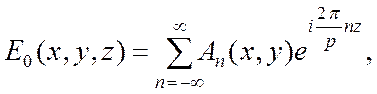                           (7.4)

где

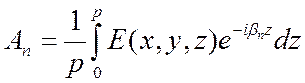                             (7.5)

Тогда поле в ЗС можно записать в виде следующего ряда

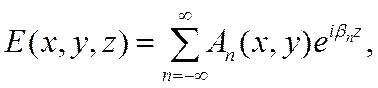                           (7.6)

где

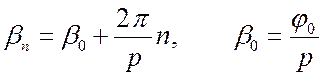                                   (7.7)

Слагаемые в ряду (7.6) называются пространственными гармониками (ПГ). – амплитуды пространственных гармоник, – их волновые числа. Нумерация осуществляется таким образом, чтобы выполнялось следующее условие для нулевой ПГ: . Обратим внимание на то, что все пространственные гармоники имеют одну и ту же частоту, равную частоте возбуждаемого в ЗС электромагнитного поля. Величина  равна изменению фазы нулевой пространственной гармоники на периоде системы, для гармоники с номером n эта величина равна .

Рассмотрим основные свойства пространственных гармоник. Определим фазовую скорость и длину волны ПГ

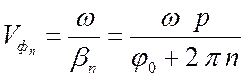                                     (7.8)

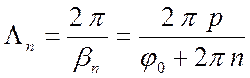                                     (7.9)

Из выражений (7.8) и (7.9) следует, что наибольшую фазовую скорость и, следовательно, наибольшую длину волны имеет нулевая ПГ. Распределение поля вдоль ЗС для различных ПГ для случая 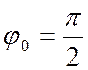 представлены на рис. 7.3.

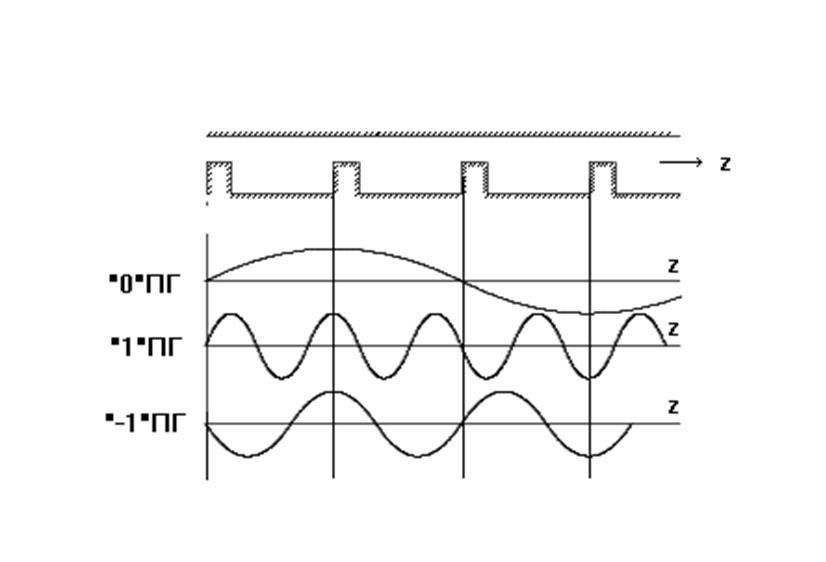
Рис. 7.3

Из формулы (7.8) видно, что пространственные гармоники с положительными номерами распространяются в направлении возрастания  (при выбранном знаке в показателе экспоненты, определяющей зависимость от времени ), а с отрицательными номерами – в обратном направлении. Направление распространения волны, соответствующей нулевой ПГ, определяется знаком . Групповые скорости всех ПГ одинаковы и равны

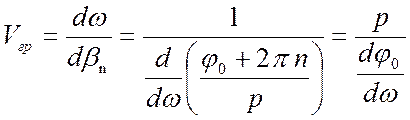.                     (7.10)

Групповая скорость равна скорости распространения энергии в ЗС и может быть определена как отношение среднего потока энергии к запасенной средней энергии электрического и магнитного поля в расчете на единицу длины

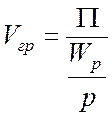.                                            (7.11)

Определим связь групповой и фазовой скорости:

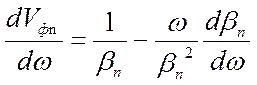,                                           (7.12)

откуда

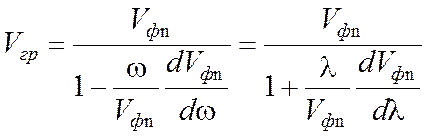.                             (7.13)