Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 2

В этом случае, как легко показать, для комплексных амплитуд   и  получаются те же комплексные уравнения (1.16), (1.17), только связь этих комплексных амплитуд с физическими полями усложняется: вместо формул (1.15) нужно применять формулы (1.18), представляя произвольный процесс в виде суперпозиции монохроматических.

1.4. Граничные условия. Теорема единственности

Параметры  и , фигурирующие в уравнениях электромагнитного поля, могут любым образом изменяться в пространстве. Это изменение может происходить не только непрерывно, но и скачкообразно, например, на некоторой поверхности S параметры могут претерпеть скачок – такая поверхность называется границей раздела двух сред. На поверхности S ЭМП также испытывает скачок,  и уравнения ЭМП должны быть дополнены граничными условиями. Как известно из электродинамики [1, 2], на поверхности раздела двух сред имеют место граничные условия

, ,                           (1.30)

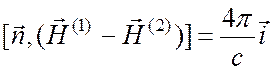,  ,                               (1.31)

где  - плотность свободного поверхностного заряда на границе раздела,  - вектор плотности поверхностного тока проводимости,  и  - произвольные касательное и нормальное к границе раздела сред направления, индексами ^{(1), (2)} отмечены поля по обе стороны границы раздела. Уравнения (1.30), (1.31) получаются из уравнений Максвелла в интегральной форме с помощью предельного перехода.

Заметим, что поверхностные электрические токи не могут существовать в проводниках, имеющих конечную проводимость. Действительно, наличие поверхностных токов означает, что через бесконечно малое поперечное сечение проводника идет конечный ток, что приведет к выделению бесконечно большого джоулева тепла. Поэтому поверхностные токи становятся физически возможными только при бесконечной проводимости тела.

1.5. Потенциалы электромагнитного поля

Потенциалы применяются в электродинамике для решения задач двух типов. Во-первых, с помощью потенциалов находится решение задачи о полях, возбуждаемых в свободном пространст­ве заданными источниками — токами и зарядами. Во-вторых, по­тенциалы позволяют решать граничные задачи электродинамики, в которых рассматриваются электромагнитные поля при наличии границ.

Употребление потенциалов электромагнитного поля значитель­но облегчает решение таких задач.

Преобразуем уравнения Максвелла. В уравнении (1.16)

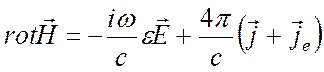,                       (1.16)

распишем  токи проводимости согласно формуле (1.7)

,                                                (1.7)

и введем комплексную диэлектрическую проницаемость среды следующим образом:

                                        (1.36)

В результате получим

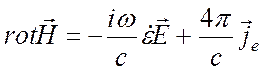,                                (1.37)

Уравнение (1.17) остается без изменений

,

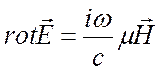Уравнения (1.3), (1.5)

,                                                  (1.3)

.                                                   (1.5)

преобразуем, воспользовавшись материальными соотношениями (1.6) и уравнением неразрывности (1.1),

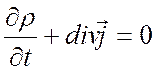,                                               (1.1)

записанным в комплексной форме.

Получим

,                          (1.38)

.                                                    (1.39)

Плотность сторонних токов  и плотность сторонних зарядов  считаются заданными.

Векторный потенциал  и магнитный потенциал  вводятся следующим образом:

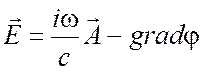,                              (1.40)

При этом оказывается, что уравнения (1.39) и (1.17) выполняются тождественно в силу основных тождеств векторного анализа (П1.7) и (П1.8) (см. Приложение 1).

Из уравнения (1.37) для однородных сред (магнитная и диэлектрическая проницаемости не зависят от координат) приходим к уравнению

,

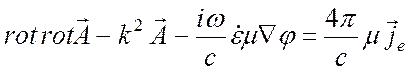где 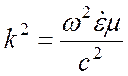 - волновое число в среде.

Или, воспользовавшись формулой (П1.6) Приложения 1,

                                            (П1.6)

приходим к уравнению

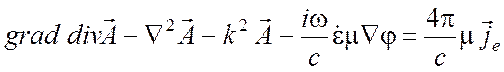                    .                         (1.41)

Учитывая произвольность функции , можно выбрать ее на основе условия, называемого калибровкой Лоренца:

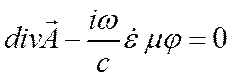                                         .                                       (1.42)