Групповая скорость отличается от фазовой только при наличии дисперсии, когда фазовая скорость пространственных гармоник зависит от частоты.
Таким образом, поле в периодической замедляющей системе, возбуждаемое гармоническим источником, представляет собой сумму бесконечного числа пространственных гармоник – волн, распространяющихся в обоих направлениях вдоль системы с разными фазовыми скоростями и одинаковыми частотой и групповой скоростью.
Физическая реальность пространственных гармоник поля периодической структуры в принципе показывается так же, как физическая реальность временных гармоник периодического сигнала. Различие состоит только в конструкции анализатора. Анализатором временных гармоник может служить высокодобротный колебательный контур; в качестве анализатора пространственных гармоник может быть использован электронный поток, который взаимодействует с полем гармоники, если движется синхронно с ней.
Заметим, что отдельные пространственные гармоники не удовлетворяет граничным условиям, что отличает их от собственных волн регулярных волноводов. Возбудить одну из них в ЗС невозможно. Поэтому, когда говорят о синхронизме электронного потока с полем ЗС, то имеют в виду совпадение скорости движения электронов с фазовой скоростью одной из пространственных гармоник.
Для конструирования ЗС важно знать ее дисперсионную характеристику, т.е. зависимость фазовой скорости (или коэффициента замедления) пространственных гармоник от частоты (длины волны). Заметим, что дисперсионные характеристики для разных пространственных гармоник различны. Знание дисперсионной характеристики позволяет определить многие важные свойства ЗС, такие как фазовую и групповую скорости, значение полос пропускания, возможность электронной настройки электронных приборов СВЧ, сопротивление связи и др.
Перейдем к рассмотрению свойств
дисперсионных характеристик ЗС. Дисперсионные характеристики будем строить в
осях ![]() , где коэффициент замедления, в
соответствии с (7.13), равен
, где коэффициент замедления, в
соответствии с (7.13), равен
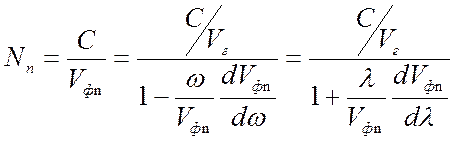 . (7.14)
. (7.14)
При условии 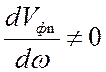 он будет зависеть от
частоты и от номера гармоники. Приведем еще одно выражение для коэффициента
замедления
он будет зависеть от
частоты и от номера гармоники. Приведем еще одно выражение для коэффициента
замедления
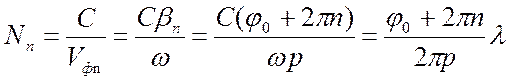 .
(7.15)
.
(7.15)
Характерной особенностью
замедляющих систем является наличие т.н. полос пропускания (прозрачности), т.е.
такого интервала частот, внутри которого возможно распространения медленных
волн, и полос непрозрачности. В этом смысле ЗС ведут себя как полосовые
фильтры. Границам полос пропускания соответствуют фазовые сдвиги ![]() и
и ![]() . Это
можно объяснить следующим образом [7]. Процесс распространения волн в ЗС
сопровождается многократным отражением от неоднородностей, отстоящих друг от
друга на период p. При указанных значениях
фазового сдвига все отраженные волны будут синфазны и волна полностью
отражается от неоднородностей. Это справедливо не только для нулевой
пространственной гармоники, но и для всех остальных. При этом значение
групповой скорости равно нулю, волны не распространяются. Рассмотрим полосу
пропускания ЗС, ограниченную длинами волн
. Это
можно объяснить следующим образом [7]. Процесс распространения волн в ЗС
сопровождается многократным отражением от неоднородностей, отстоящих друг от
друга на период p. При указанных значениях
фазового сдвига все отраженные волны будут синфазны и волна полностью
отражается от неоднородностей. Это справедливо не только для нулевой
пространственной гармоники, но и для всех остальных. При этом значение
групповой скорости равно нулю, волны не распространяются. Рассмотрим полосу
пропускания ЗС, ограниченную длинами волн ![]() и
и ![]() . Покажем, что на границах полосы
пропускания дисперсионные характеристики идут вертикально. Перепишем выражение
для групповой скорости, учитывая
. Покажем, что на границах полосы
пропускания дисперсионные характеристики идут вертикально. Перепишем выражение
для групповой скорости, учитывая
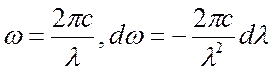 ,
,
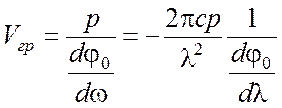 . (7.16)
. (7.16)
Так как на границах полосы пропускания групповая скорость
равна нулю, то на этих частотах 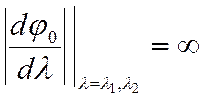 . Продиффеенцировав выражение
(7.15) по
. Продиффеенцировав выражение
(7.15) по ![]() , получим
, получим
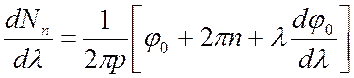 .
(7.17)
.
(7.17)
Отсюда следует, что 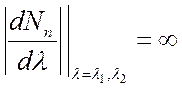 . Из (7.16)
следует еще одно свойство: в пределах полосы пропускания функция
. Из (7.16)
следует еще одно свойство: в пределах полосы пропускания функция ![]() может либо монотонно возрастать, либо
монотонно убывать, т.к. точке экстремума соответствовало бы бесконечное значение
групповой скорости.
может либо монотонно возрастать, либо
монотонно убывать, т.к. точке экстремума соответствовало бы бесконечное значение
групповой скорости.
Приступим к построению
дисперсионных характеристик, основываясь на выражениях (7.14) и (7.15). Из
(7.15) следует, что дисперсионные характеристики пространственных гармоник
располагаются в областях, определяемых полосой ![]() и
лучами
и
лучами 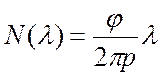 , где
, где ![]() и
и ![]() для первой гармоники, где
для первой гармоники, где ![]() и
и ![]() , для
второй гармоники,
, для
второй гармоники, ![]() и
и ![]() , для минус
первой гармоники и т.д.
, для минус
первой гармоники и т.д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.