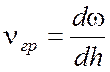Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 17

.                                         (3.66)

Формула (3.66) является общей формулой, позволяющей рассчи­тывать групповую скорость распространения сигнала в любой системе. Един­ственным условием применимости этой формулы является требо­вание, чтобы спектр сигнала, схематически изображенный на рис. 3.10, был сосредоточен в достаточно малом диапазоне вблизи про­извольной центральной частоты .

Вычисляя по формуле (3.66) групповую скорость электромаг­нитной волны в волноводе, получаем

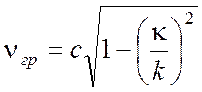.                                      (3.67)

Таким образом, групповая скорость волн в волноводе оказывает­ся, как это и следовало ожидать, всегда меньше скорости с. По­скольку , то относительно наблюдателя, движущегося вместе с огибающей (со скоростью ), синусоида высокочастотного за­полнения будет двигаться вперед; при этом передние гребни си­нусоиды будут исчезать, доходя до передней границы сигнала, а задние гребни - возникать в «хвосте» сигнала. Интересно, что фазовая и групповая скорости в волноводе удовлетворяют соот­ношению

.(3.68)

Глава 4. Потери в волноводах

4.1. Волноводы, заполненные веществом

Выше рассмотрены свойства волноводов в предположении, что пространство внутри волновода имеет электромагнитные свой­ства пустоты. В ряде случаев интересно знать, как изменяются свойства волновода при его заполнении однородным веществом с произвольными электродинамическими параметрами. Обозначим через  и  комплексные диэлектрическую и магнитную проницаемости однородной среды, заполняющей волновод. Продоль­ное волновое число в пустом волноводе

                                      (4.1)

где - поперечное волновое число, зависящее лишь от геомет­рии волновода, h – продольное волновое число.

При переходе к волноводу, заполненному веществом, следует заменить волновое число k  для пустоты комплексным волновым числом  в веществе, и тогда

.                                  (4.2)

Отсюда видно, что, заполняя волновод диэлектриком с вещест­венным значением Re > 1 и  = l, получаем возможность переда­вать по волноводу более длинные волны. Действительно, распро­странение волны в волноводе без заполнения возможно лишь при: k >, а с диэлектрическим заполнением - при k >  - волна будет распространяться при частотах более низких.

Если среда, заполняющая волновод, имеет потери, т. е. прони­цаемость  или  имеет заметную мнимую часть, то при любых соотношениях между рабочей длиной волны и поперечными раз­мерами волновода данная волна в волноводе имеет комплексное продольное волновое число h, как это следует из формулы (4.2). В этом случае нельзя провести четкого разделения волн в волноводе на распространяющиеся и затухающие, поскольку распространение волн неизбежно связано с затуханием, так как при распространении возникают потери в веществе. Чисто зату­хающих волн при этом тоже нет, так как из-за потерь в среде все волны переносят активную мощность и обладают некоторой скоростью распространения.

Сказанное можно проиллюстрировать следующими рассуждения­ми. Положим

                                  (4.3)

где и  вещественны и положительны; тогда формула (4.2) приобретает вид

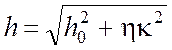                                             (4.4)

и, если величина  мала по абсолютной величине, то можно воспользоваться разложением

.                                       (4.5)

Если h₀ > 0 и  = i||, то поправочный член в формуле (4.5) чисто мнимый, он определяет затухание распространяющейся вол­ны. Если же h₀ = i| h₀| и  = i||, то поправочный член веществен­ный, он дает для затухающей волны малую вещественную часть продольного волнового числа, т. е. конечную фазовую скорость.

Однако, формула (4.5) применима только при  и вблизи критической  частоты, когда | h₀|  0, дает неправильные результаты, в то время как формула (4.4) применима при лю­бых частотах и при h₀ = 0 дает простой результат h = .