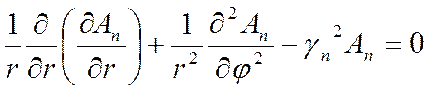Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 38

.                     (7.26)

Решение этого уравнения будем искать в виде

.                                    (7.27)

Подставляя (7.27) в (7.26), получим

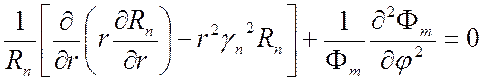.                     (7.28)

Решение для  имеет вид

                           (7.29)

Уравнение для  принимает вид

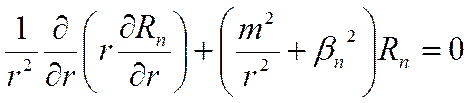                        (7.30)

Решением этого уравнения является линейная комбинация модифицированных функций Бесселя первого и второго рода порядка :

 .                       (7.31)

Общее решение уравнения (7.26) можно теперь представить в виде

.               (7.32)

Для спиральной ЗС в свободном пространстве с учетом конечности поля на оси спирали и его стремления к нулю на бесконечности получим, что внутри спирали поле описывается функцией

,                                  (7.33)

а вне спирали

.                                (7.34)

И внутри, и вне спирали поле затухает при отходе от ее поверхности, как и в рассмотренном выше случае гребенчатых структур. Причем чем больше номер гармоники, тем сильнее поле прижато к поверхности спирали. Аналогично поле ведет себя и для других типов ЗС.

Поверхностный характер распределения поля в ЗС необходимо учитывать, например, при определении места прохождения электронного пучка для обеспечения эффективности его взаимодействия с СВЧ полем при конструировании электронных усилителей и генераторов.

Для количественной оценки эффективности взаимодействия электронного потока с полем вводят специальную характеристику ЗС – сопротивление связи, причем эта характеристика относится к выбранной пространственной гармонике. Если, например, электронный пучок перемещается вдоль координаты , то для гармоники с номером сопротивление связи определяется следующим соотношением

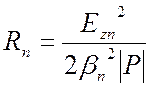.                                        (7.35)

То есть сопротивление связи выражает отношение квадрата амплитуды напряженности соответствующей составляющей электрического поля к мощности, переносимой через поперечное сечение ЗС всеми пространственными гармониками.

Приведенное выражение для сопротивления связи можно получить из рассмотрения аналогии между ЗС и длинной линией. В длинной линии поток энергии связан с амплитудой напряжения и волновым сопротивлением следующим образом

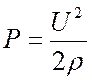.                                                 (7.36)

Волновое сопротивление определяется отношением «поперечного» напряжения бегущей волны к току: 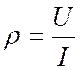. Нас же интересует продольная составляющая поля. Поэтому напряжение заменяют интегралом от продольной составляющей поля, вычисленному на интервале изменения поля от нуля до максимума:

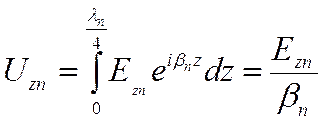.                        (7.37)

Заменяя в (7.36)  на  и  на  получим (7.35).

Для вычисления сопротивления связи нужно знать распределение поля и дисперсионную характеристику. Поток энергии можно вычислить, проинтегрировав вектор Умова-Пойнтинга по поперечному сечению ЗС, а волновое число определить из дисперсионной характеристики для заданной частоты. Величину  нужно подставлять для той части сечения, где проходит электронный поток. Практически сопротивление связи рассчитывается либо на оси системы (для спиральных ЗС), либо вблизи поверхности (для гребенчатых и штыревых ЗС). Типичные значения сопротивления связи лежат в пределах от десятков до сотен Ом.

8. Методы расчета ЗС.

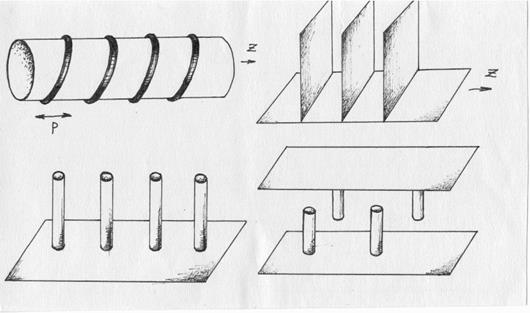
Метод ЧО на примере пластинчатой гребенки.

Декартова СК

Компоненты электромагнитного поля:

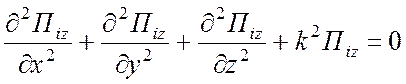
Поле ТМ типа относительно z -

, , ,

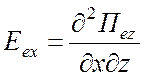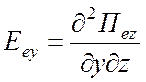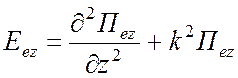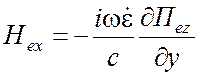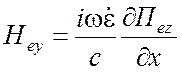, , ;                 (1.69)

Поле ТЕ типа относительно z -

, ,  ,

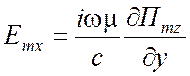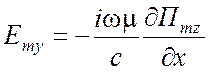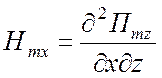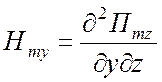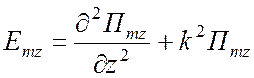, , .              (1.70)

Будем искать решение Е типа:

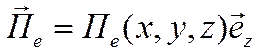
С учетом пространственной периодичности ЗС и в предположении независимость поля от y

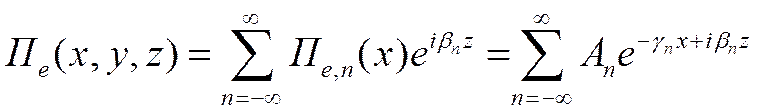
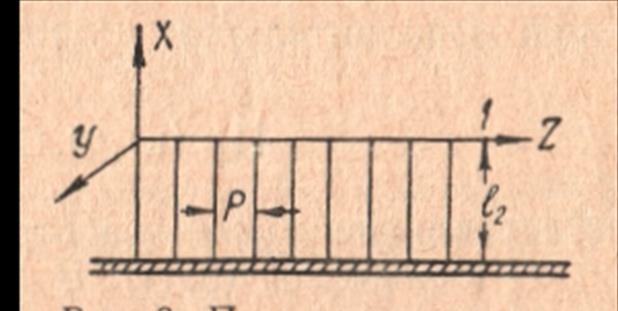
Область I – над пластинами.

Предположим, что 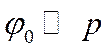. В этом случае будет преобладать нулевая ПГ

 

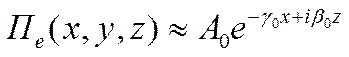
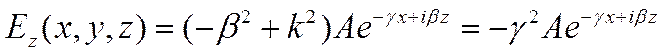
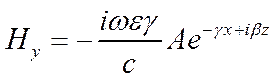
II область – между пластинами. Пренебрежем зависимостью поля от Z.

    

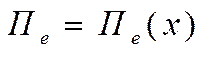
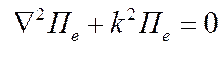
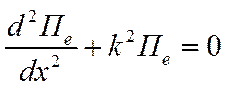
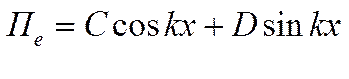
Определим касательные компоненты поля