Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 29

6.2. Ортогональность собственных волн в волноводе

До сих пор мы исследовали распространение электромагнит­ных волн в средах как решения однородных уравнений Максвелла, т.е. как бы в отрыве от ис­точников этих волн. Таким путем изучены свойства волн, которые могут существовать в некоторой системе. Для практики важно, однако, знать, какое электромагнитное поле создается под воздействием источника поля, с какими амплитудами возбуждаются различные волны и т. д.

Поэтому нельзя ограничиваться исследованием свободных или собственных колебаний (волн), удовлетворяю­щих однородным уравнениям поля (без источников)

,  .                              (6.20)

Необходимо   исследовать  также  вынужденные  электромагнитные колебания  данной  системы  под действием  источников  поля.  Задавая эти источники в виде сторонних электрических и магнитных токов с плотностями  и , следует решать неоднородные урав­нения электромагнитного поля

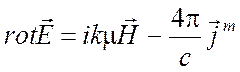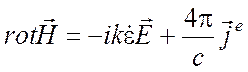,  .              (6.21)

Оказывается, что задача о вынужденных колебаниях легко ре­шается, если более простая задача о свободных колебаниях реше­на полностью и известна полная система решений однородных уравнений (6.20). Покажем это.

Рассмотрим электромагнитное поле в обобщенном регулярном волноводе. Если волновод образован идеально проводящей стенкой, то на ее внутренней поверхности S₀ имеет место граничное условие

 = 0 на S₀                                        (6.22)

и все электромагнитное поле заключено внутри S₀. Если учиты­вать конечную проводимость стенки волновода, то на поверхности стенки S₀ нужно ставить граничное условие Леонтовича (4.8)

 на S₀ ,                              (6.23)

и электромагнитное поле будет слегка просачиваться за пределы по­верхности S₀ на расстояния порядка толщины скин - слоя d. Здесь Z есть комплексный волновой импеданс металлической стенки;  - нормаль к поверхности S₀, направленная внутрь металла.

В случае металлической стенки можно выбрать цилиндричес­кую поверхность S₀ иначе, а именно, проводя S₀ внутри стенки на глубине, значительно превышающей толщину скин - слоя, по­лучим приближенное условие

на S₀,                                     (6.24)

выражающее тот факт, что все электромагнитное поле заключено внутри S₀.

Будем считать волновод бесконечным и однородным по оси z, так что проницаемости ,  суть функции х, у, не зависящие от z (это относится как к веществам, заполняющим волновод, так и к материалу стенок). Тогда,  частные решения уравнений (6.20) имеют зависимость от координаты z в виде e^ihz (см. гл.3). Такие решения являются собственными волнами рассматриваемой системы. Пред­положим также, рассматриваемый волновод имеет диск­ретный спектр собственных волн. Иначе говоря, все волны в дан­ном волноводе могут быть объединены в одну последовательность так, что волна с номером s имеет поле E_S, H_s и волновое число h_s, т.е. зависит от z посредством множителя . Положительные индексы s (s = 1, 2, ...) имеют волны, распростра­няющиеся   в   направлении   поло­жительной оси z,  точнее, имею­щие Im h_s  > 0. Во избежание со­мнений будем  считать   (как при доказательстве   теоремы   единсвенности  в § 1.4), что волновод имеет потери, так что незатухаю­щие волны, для которых Im h_s  = 0, в нем существовать не могут. Отрицательным индексом - s (s > 0) обозначаем такую же волну, что и с номером s, но распространяющуюся в противоположном направлении; ее волновое число h_s = - h_s.

Общее  решение уравнений (6.20) имеет вид

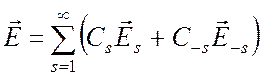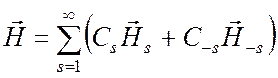,    ,                  (6.25)

где C_s и C_-s - произвольные постоянные, одинаковые для электрического и магнитного поля. Отметим, что индекс s можно рассматривать как краткую запись группы других индексов. Так, например, в волноводах с иде­ально проводящими стенками и однородным заполнением индекс s или - s заменяет обычные символы Е_sп или Н_sп и указание направления распространения волны.