Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 31

Тогда

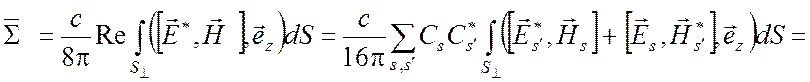 (6.38)

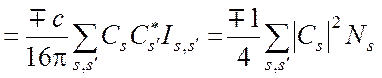
т.е. полная колеблющаяся мощность, переносимая суммой волн через по­перечное сечение волновода, равна сумме колеблющихся мощнос­тей, переносимых каждой волной в отдельности: взаимная колеб­лющаяся мощность волн с индексами s и s' равна нулю.

Для волн в идеальном волноводе, рассмотренных в гл. 3, ортогональность можно сформулировать так же, как равенство ну­лю комплексных мощностей различных волн, а норма пропорцио­нальна  комплексной  мощности,  переносимой  волной.

Покажем, что от условия ортогональности для векторных полей можно перейти к условиям ортогональности для собственных функций волноводов

Сначала рассмотрим ТМ поле и воспользуемся выражениями для электрического и магнитного полей (3.9), (3.10)

, .

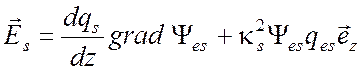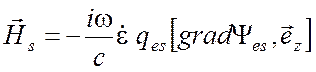Возьмем условие ортогональности в виде (6.35) и вычислим z - ую проекцию векторного произведения

.

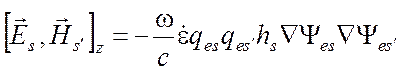Действуя аналогично, получим выражения для ТЕ поля на основе формул (3.15), (316):

, .

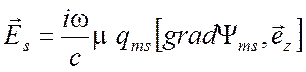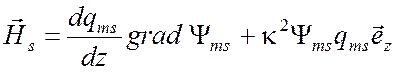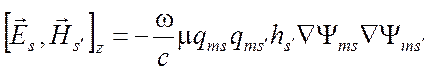
Таким образом, имеем

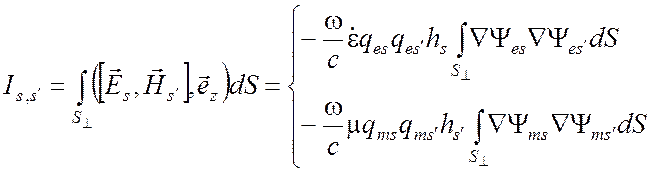
Преобразуем  интеграл по поперечному сечению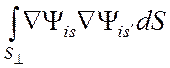. Для этого воспользуемся известным из векторного анализа равенством

а также уравнением (3.7) для собственных функций .  Тогда

.

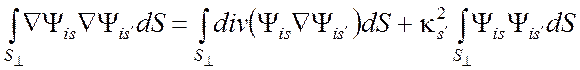Первый интеграл в этом равенстве, который мы преобразовываем с помощью теоремы Гаусса - Остроградского 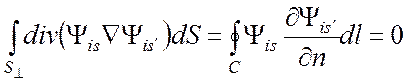, оказывается равным нулю на контуре интегрирования для всех случаев в силу граничных условий (3.11), (3.17) для электрической и магнитной мембранных функций. В результате, имеем

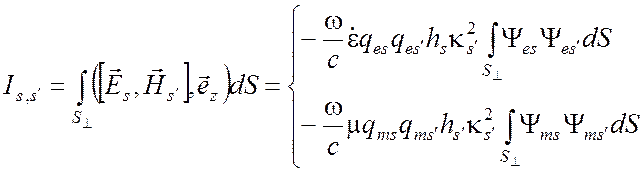
Таким образом, условие ортогональности для векторных полей совпадает с условием ортогональности для собственных функций волновода.

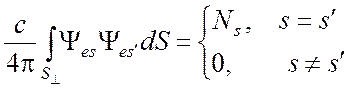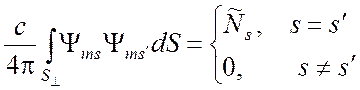, ,     (6.39) 

где , .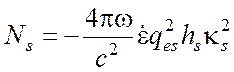

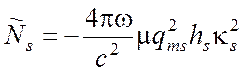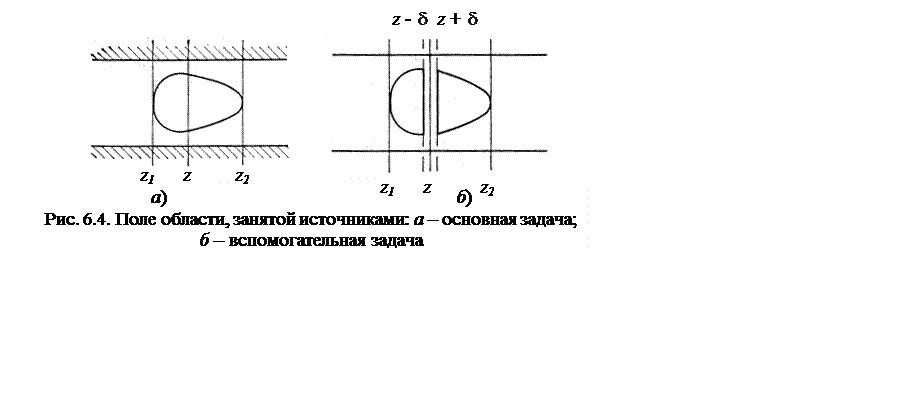
6.3. Возбуждение бесконечного регулярного волновода

Предположим, что все источники поля (электрические и маг­нитные токи) находятся при z₁ < z < z₂. Так как при z <z₁ и z > z₂ искомое электромагнитное толе удовлетворяет однородным уравнениям (6.1), то оно должно иметь вид (6.25). Однако поле, возбуждаемое данными источниками, должно при z  стремиться к нулю вследствие потерь в волноводе; только при этом дополнительном условии согласно § 1.4 получается единст­венное решение электродинамической задачи. Поэтому справа от источников

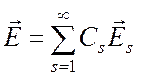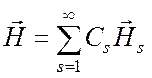,    (при z > z₂),                 (6.40)

а слева от источников

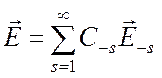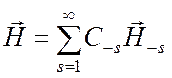,       (при z < z₁).(6.41)

Таким образом, волны должны расходиться от области, занятой источниками. Комплексные амплитуды этих волн (коэффициенты C_s и C_-s)легко найти, если воспользоваться леммой Лоренца (6.5), в которой вместо поля  взять искомое поле , удовлетворяющее уравнениям (6.21), а в качестве поля  - сначала поле , а затем поле  (счита­ем s' > 0). Поверхность S выберем так же, как и раньше (см. рис. 6.3), причем возьмем поперечное сечение S₁ левее всех ис­точников, т. е. при z < z₁, а сечение S₂ - правее всех источников, при z > z₂. В результате получим соотношения

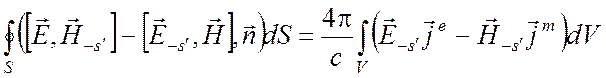,          (6.42)

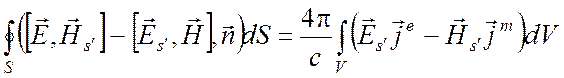
Интеграл по поверхности S₀ обращается в нуль по тем же причи­нам, что и раньше. На сечениях S₂ и S₂ векторы  представ­ляются в виде рядов (6.40) и (6.41). Из условия ортогональнос­ти (6.29) и формулы (6.30) вытекает, что

,

,

,

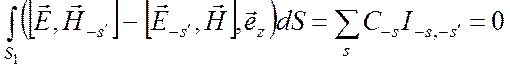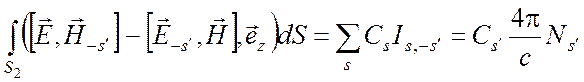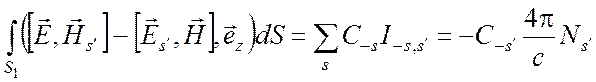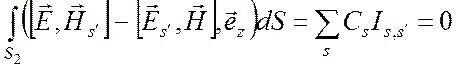
Окончательно получаем следующие формулы:

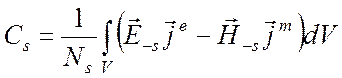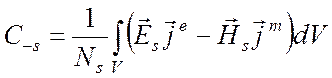, ,       (6.44)

определяющие коэффициенты C_s и C_-s в виде интегралов по объ­ему, занятому источниками. Таким образом, волна, распространяющаяся направо, определяется всеми источниками, которые расположены левее, и, аналогично для волны, распространяющейся налево. Заметим, что C_s и C_-s получились постоянными (не зависящими от z), как это и предполагалось при написании формул (6.40) и (6.41).

Выведенные выражения имеют простой и наглядный вид. Их недостаток заключается в том, что в области z₁ < z < z₂, занятой источниками, они неприменимы. Для определения электромагнит­ного поля при некотором z, лежащем между z₁ и z₂ (рис. 6.4,а), можно воспользоваться следующим приемом: мысленно удалим (рис.6.4,б) источники из плоского слоя (z - , z + ) и обозначим получающееся в сечении z электромагнитное поле через . Поле  есть, в сущности, поле в области, свободной от источ­ников, поэтому его можно представить в виде (6.25). По сообра­жениям, приведенным выше, электромагнитные волны, распрост­раняющиеся направо , создаются источниками, находящи­мися слева от данного сечения z а волны, распространяющиеся налево , - источниками, расположенными справа. По­этому в пределе при  получаем