Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 7

Среди проводников наибольшее практическое значение имеют металлы. Если ограничиться сначала неферромагнитными метал­лами, то можно сказать, что электродинамические свойства метал­лов определяются исключительно их проводимостью. Как показы­вает опыт, проводимость металлов при всех радиочастотах (вплоть до миллиметровых волн) практически сохраняет то же значение, что при постоянном токе. В оптическом диапазоне (начиная с инфракрасных волн) электрические свойства металлов усложняются.

Комплексная диэлектрическая проницаемость металлов имеет весьма большую мнимую часть . Действительно, для меди имеем удельное    сопротивление  = 1,7-10⁶ Ом-см, откуда в абсолютной системе единиц проводимость  = 5-10¹⁷ с^-1 ( = 9-10¹¹/). Даже для висмута, являющего­ся полуметаллом и сравнительно плохим проводником ( = 1,2- 10^-4 Ом-см), имеем  = 7,5-10¹⁵ с^-1, в то время как для световых волн частота f ~ 5-10¹⁴ Гц. Поэтому для всех металлов во всем диапазоне радиочастот и отчасти даже при оптических ча­стотах величина является весьма большим числом, по сравнению с которым вещественной частью  комплексной диэлектрической проницаемости можно практически пренебречь. Поэтому для металлов обычно полагают

.                                             (2.15)

Комплексное волновое число в металле

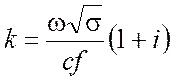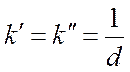, ,                                  (2.16)

где для d - глубины проникновения поля в металл - можно написать выражение:

.

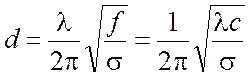Для меди d  = 0,4 мкм при  = 1 см, d = 4 мкм при  = 1 м, d  = 40 мкм при  = 100 м и d  = 0,4 мм при  = 10 км.

Глава 3. Волны в регулярном волноводе

3.1. ТМ и ТЕ волны в регулярном волноводе

Волноводом называется некоторая идеальная система, представляющая собой полый металлический бесконечный цилиндр, име­ющий поперечное сечение произвольной формы. Внутри цилиндра находится вакуум. Будем искать решение уравнений Максвелла в регулярном волноводе, т.е. в волноводе, поперечное сечение которого неизменно.

Введем обобщенную цилиндрическую систему координат .  Определим структуру поля в таком волноводе без источников. Математическая постановка задачи формулируется в виде однородных уравнений Максвелла - уравнений (1.49), (1.50) без источников

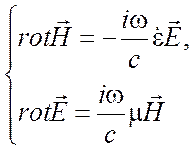                                                    (3.1)

и граничных условий на идеально проводящих стенках волновода

= 0 на С,                                                    (3.2)

где С – контур, получающийся при пересечении волновода с плоскостью z = const.

Для построения решения воспользуемся принципом поляризационной двойственности (см. § 1.6). Решение системы однородных уравнений Максвелла для однородных сред может быть представлено суперпозицией фундаментальных решений ТМ и ТЕ типа относительно координаты разделения  z. При этом каждое ТМ и ТЕ решение описывается однокомпонентным электрическим (или магнитным) вектором Герца, направленным по координате z:

, ,                                          (3.3)

где  - единичный орт в направлении координаты z. Вектора Герца удовлетворяют дифференциальным уравнениям в частных производных

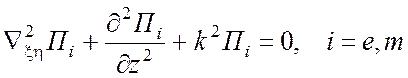,                           (3.4)

где 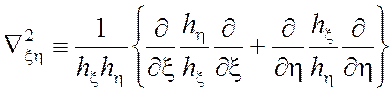 - поперечная часть оператора Лапласа, 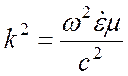 - волновое число.

Для построения решения уравнений (3.4) воспользуемся методом разделения переменных. Будем искать вектора Герца  в виде произведения

.                                           (3.5)

Подставим выражения (3.5) в уравнения (3.4) и разделим их на величину . Приходим к уравнениям

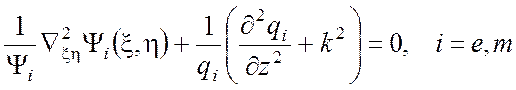                          (3.6)

Так как первое из слагаемых в уравнениях (3.6) зависит от координат , а второе  - от координаты z, то  равенство нулю удовлетворяется только в том случае, если каждое из слагаемых равно константе. В результате приходим к системе уравнений:

,                                                   (3.7)

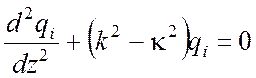,                                               (3.8)

где ,   - поперечное волновое число, h – продольное волновое число, функция  называется мембранной функцией и  q_i(z) – волновой функцией.

Решением уравнения (3.8) является совокупность двух функций

,