Поэтому говорят, что назрев проводников зависит от плотности тока, причем платностью тока называется число ампер, приходящееся на каждый квадратный миллиметр площади поперечного сечения проводника. Так, например, если проводник имеет площадь ;нопоречного сечення 4 кв. мм и по нему проходит ток, силой20 ампер, то плотность тока в этом проводнике равна: * ' ■
— = 5 ампер на 1 кв. мм.
Если бы по этому проводнику проходил ток, силой 12 ампер, т# плотность тока в нем была бы равна:
12
— = 3 ампера на 1 кв. мм.
Итак, нагрев проводников зависит от плотности тока, и само собой разумеется, что с увеличением плотности тока проводники будут сильнее нагреваться. Поэтому на практике назначают предельную (наибольшую) плотность тока, допускаемую в проводниках для безопасного их нагрева. Несомненно, что эта предельная плотность тока зависит от того, голый ли проводник, или он изолирован, а если он имеет изоляцию, то на-.'!.. сколько эта изолирующая оболочка может выдерживать высокую температуру. Так, например, в голых проводниках может быть допущена большая плотность тока, чем в изолированных. В проводниках с резиновой изоляцией не должна допускаться температура пагрова свыше 50°Ц, а потому при определении допустимого значения силы тока в изолированных проводниках при данном- поперечном сечонии пользуются особой таблицей, рассчитанной на нагрев проводника до температуры не свыше 50° Ц.
Таблица наибольшей допустимой силы ток» в изолированных медных проводах и кабелях, не проложенных в земле.
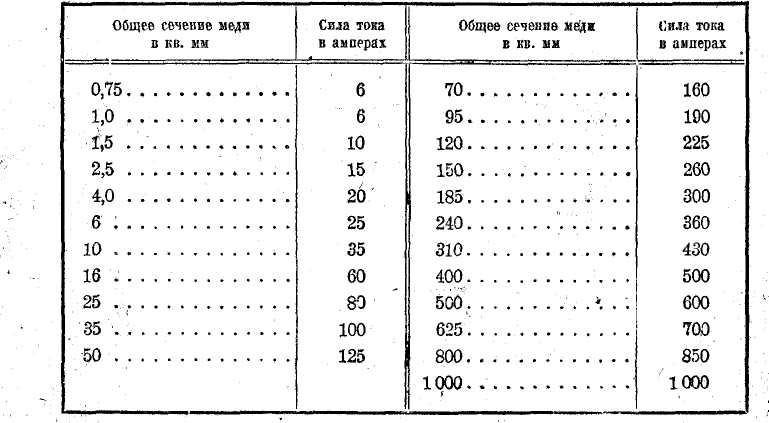
Как видно яз таблицы, в проводнике сечением в 1 кв. мм допускается плотность тока 6 4 на 1 кв. мм, в проводнике сеченном в
80 25 кв. мм плотность тока допущена ^ = 3,2 А на 1 кв. мм, в про-
воднике сечением 400 кв. мм плотность тока не должна превышать
500
-г—• = 1,25 А на 1 кв. мм, и, наконец, в проводнике сечением 1000 кв. мм
1000 1 А
допускаемая плотность тока равна только vTwT= * ■**■ на 1 кв. мм.
j - 1 UOO
Неодинаковая допускаемая плотность тока объясняется тем, что толстые ■ проводники сильнее нагреваются, чем тонкие, так как они имеют относительно меньшую поверхность охлаждения. Действительно, возьмем, например, один проводник, сечением 35 кв. мм, и пропустим через него ток, силой 100 ампер; он будет нагреваться, положим, до 50° Ц. Если же взять проводник сечением в 70 кв. мм, то через него нельзя пропустить 200 ампер; приходится ограничиться'током силой в 160 ампер; в противном случае нагрев проводника превзойдет допустимую для проводника с резиновой изоляцией величину.
Для проводников железных, манганиновых и других может быть допущена значительно большая плотность тока, в особенности в тех случаях, когда эти проводники не покрыты изолирующей оболочкой.
Так, например, хромониккелевая проволока (из нихрома), применяемая в электрических печах *и других нагревательных приборах, при диаметре в 0,5 мм выдерживает ток силой 4 ампера; при диаметре в • 0,4 мм силу тока снижают до 2,6 А, а при диаметре 0,3мм сила тока не может быть допущена свыше 1,5 А. Не трудно подсчитать, что плотность тока в нихромовой проволоке принята до 20 А на 1 кв. мм.
Если применить идя этих целей железную проволоку, то при диаметре 0,5 мм может быть допущен ток в 5, а при диаметре в 6 мм — ток в 10 ампер.
П р и м е р 43, При помощи микрометра* измерен диаметр медной проволоки; он оказался равным 2, 6 мм. Проводник изолированный и предназначен для установки на изоляторах. Определить наибольшую допустимую силу тока в этом проводнике. .
'Решение. Мы знаем, что поперечное сечение Sпроводника может быть п определено, если известен его диаметр d, по формуле:
![]() ,4 4
,4 4
До таблице, приведенной на стр. 80, находим, что наибольшая допустимая величина силы тока в этом проводнике равна 25 а м д е р а м.
Пример 44.
Рассчитать электрическую грелку на 4 ампера для напряжения
110 вольт
Если У=« 110 вольт и ток /==4 ампера, то сопротивление грелки долм» быть равно:
Удельное сопротивление нихрома (см. стр. 68) равно 1,1, а потому сопротивление 1 м проволоки, сечением 0,2 кв. мм, будет равно
g = 5,5 ом.
Следовательно, для данной грелки требуется проволока длиной
, 27,5 се
^=-§j = 5>5 метра. У
§ 42. Мощность н отдача источника электрического тока. W
Когда источник электрического тока включен в цепь, он развивает электрическую мощность, которая и расходуется как во внешней цепи, так и внутри этого источника, переходя в последнем в тепло. Полезной электрической мощностью источника называют мощность, расходуемую им во внешней цепи, в отличие от полной развиваемой источником электрической модности. Очевидно, что полезная мощность всегда меньше полной, и числе», показывающее, во сколько раз полезная электрическая мощность меньше полной, называется коэффициентов' полезного действия данного источника или его отдачей. Не трудно видеть, что коэффициент полезного действия всегда меньше единицы. Иногда коэффициент полезного действия выражают в процентах,- для чего его умножают на 100.
Коэффициент полезного действия обыкновенно принято обозначать
греческой буквой ■»]. /
Пример 45. В цепь гальванического элемента с электродвижущей силой 1,4 вольта и внутренним сопротивлением 0,5 ома включено внешнее сопротивление,' равное 2,3 ома. Найти полную и полезную электрическую мощность элемента в ■ коэффициент его полезного действия.
Решение. Дано: 2?= 1,4 вольта; Д0 = 0,5 ома; jRi = 2,3 ома. i
По закону Ома, сила тока в цепи равна: !
Полная электрическая мощность, развиваемая элементом, равна
У ' В \ I—1,4 X 0,5 = 0,7 ватта.
Полезная электрическая мощность, расходуемая во внешней Цепи, равна:.\
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.