Электротехника \ Электротехника

Основы электротехники сильных токов. Электрические и магнитные явления, страница 13

Так как

■ :i-'.-:"-'"    ...   ,'■■■*   ■■    ■         ■ ' >■ ■    ■'       ' ,' ■ 'л

то теперь мы можем,дать новое определение единицы эдектричесвдо

напряжения:

JВольт есть такое   электрическое  напряжение, которое,

У проводнике, имеющим сопротивление в один ом, производит

ток силою один ампер.                      

, Пример 7. Вольтметр, присоединенннй к койцам сопротивления (рис. 66),
показал 20 вольт, (^пределить силу тока в цепи, если известно, что сопротивление
It равно 4 омам.                                                                                             ;

Решение. Дано: R=4Q и V==20 вольт.

Йо формуле закона Ома найдем:                                                           •/


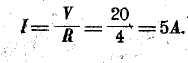
Прпжер 8. Чороз катушку проходит злектрпчоокий ток, силой 2 ампера;-вольтметр, пршшочошшй к концам катушки, локоаил 100 иолы. Уаиать сопрс*-тввденне катушки.

Рвшвние. Дапо: 1=2А и У =100 мольт. Напишем Формулу закона Она:

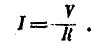
йа этой формулы получим:


§ 24. Закон Оиа для всей цени.

Рассмотрим электрическую цепь, состоящую из гальяапичоского
элемента и внешнего сопротивления. Германский ученый Ом заметил
простую зависимость между электродвижущей силой, оялой токаи
электрическим сопротивлением, которую и назвали законом Ома:
«5 Сила тока равна электродвиоюущей силе, разделенной на по$~
Ъе сопротивление всей цепи.                                                        4,K(rf

"Если обозначить электродвижущую силу буквой Д силу тавйг' буквой 1, а полное сопротивление буквой Л, то закон Ода можно ьы\ разить формулой:

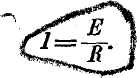
Если электродвижущая сила выражена в вольтах, сопротивление в омах, то по разделению числа вольт на число ом получим силу тока в амперах.

Мы уже говорили в § 20, что полное сопротивление Л всой цепи состоит из двух слагаем&х, т. е.

где ^j—внешнее сопротивление, a i?0 (сопротивление самого, элемента).

Следовательно, в общем виде формула закона Ома может быть на-
висана следующим образом^»*»*»*™»**^     .            .

—,,внутреннее сопротивление


Р в щ « н и в. Дано: йд == 3,8 2, До = 1Д 2

280 /= 280 миллиампер =   „ - ампера = 0,28 ампера.

Пеашое сопротивление цепи:

R«= й, + До = 3,8 +1,2 = 5 ом.
По закону. Ома имеем:                                •

/= -J-, или 0,28 = -|-,


Пример 11. Напряжение-электрической установки равно 110 вольт. В цепь-включен, электрический чайник, и при помощи амперметра узнали, что череж чайник проходят ток, силой 4 ампера. Определить -сопротивление эл.ектричееадж' чайника.

. '   Решение. Дано: 7=110 вольт,'#*=£ампера.

По формуле закона Ома для участка цепи имеем: 1==-^-, откуда:

Отсюда 1южно определить В:'


Пример 12. На электричеекойстаяцйи поддерживается напряжение, равное^
112 вольтам. Для освещения завода проложены провода, сопротивление которых,
равно ОД ома.' Определить напряжение в цепи на заьо'де, если по провода^ нро-^
ходит ток, силой 50 ампер.                                                                        .              .

Решение. Дано: F= 112 вольт, /==50 A, R =0,1 ома. V Падение напряжения в проводах равно: ~

R х /= ОД X 50 = 5 вольт.

Напряжение F, на заводе будет меяьще, чем напряжешге 7 на станции, щц веотчину падения напряжения в проводах от станции до завода:

Яр и мер 13. Напряжение установки равно 110 вольт. Определить сопротивление, необходимое дда включения в цепь лампы кинематографического аппарата, требующей для своего горения ток силой 30 ампер и напряжение 50 вольт.

Решение. Лампа требует ток силой 30 ампер, ири напряжении на зажимах, равном 50 вольтам, а наша установка имеет напряжение 110 додыу Следо­вательно, является необходимым ввести в цепь лампы такое сопротивление Я*. в котором происходило бы падение напряжения:

Но ста тока / известна и равна 30 амперам, а потому сопротявлейяй &
мшхо: •                                                             .  ' '                                   .      '■■■■,■'■                                                          ,


Следует обратить внимание на то обстоятельство, ато сопротивление Д (рис. 67)" может быть по желанию включено или в плюсовый или в минусовый провод, так как все равио оно будет выполнять свое назначение и в нем будет происходить тре­буемое падение напряжения^


<§ 25. Зависимость между электродвижущей силой элемента и" напряжением на его зажимах.

Рассмотрим цепь гальванического элемента, замкнутого на какое-нибудь внешнее сопротивление // (рис. 68); буквами А ж Л обозначим зажимы элемента, к которым присоединен вольтметр У. '

Вольтметр У, присоединенный так, как показано на рис. 68, изме­ряет напряжение на зажимах элемента. Но, с другой етороны» ■этот же вольтметр приключен к концам внешнего спротквления Ви а потому он должен показать падение напряжения во внешней цепи;

где /— сила тока в цепи элемента.

Применим теперь закон Ома для всей цепи:

Е

откуда:

В этом выражении первое слагаемое представляет вобою падение
напряжения во внешней цепи, а второе слагаемое /•/?„ есть не что
иное, как падение напряжения внутри элемента.                    ( •■

Итак,; электродвижущая сила , элемента равна сумме падений на-

, пряжений во внешней цепи и внутри элемента. Другими словами,

*Э|©щюдвижущая сила расходуется на преодоление внутреннего • со-

■■ 'приживления элемента и на прййгДоленив сопротивления внешней- цепи.

"Но мы уже видели, что падение напряжения во внешней цепи

равно напряжению У на зажимах элемента, а потому       ,     .

Это равенство показывает нам, что в замкнутой цепи электродви­жущая сила больше напряжения Vна, зажимах элемента на величину падения напряжения внутри элемента.

Скачать файл