Основы электротехники сильных токов. Электрические и магнитные явления, страница 20

; это значит, что один метр медной проволоки с поперечным сечением в 1 кв. мм обладает сопротивлением в — ома.

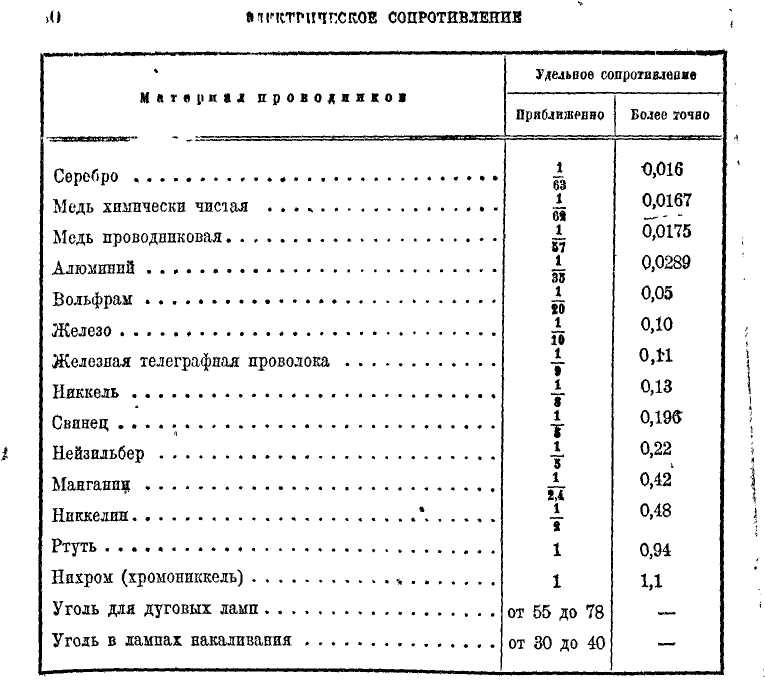
В приводимой таблице (см. след. стр.) указаны удельные сопроти­вления наиболее часто применяемых в технике материалов.

Удельное сопротивление принято обозначать греческой буквой р,

Само собой разумеется, Что удельная проводимость меди будет равна= 57. Р

¹ Поперечным сечением проводника, называется та площадь, которая, полу­чится, если проводник разрезать поперек. Если проводник круглый, то поперечное сечение его будет кругом; если же проводник прямоугольной, то попереч­ное сечение его будет прямоугольник. Для того чтобы узнать площадь поперечное, того сечения круглого проводника, надо вычислить площадь круга, а потому дм этого нужно знать толщину проводника, его диаметр.

Если обозначить буквами: R— сопротивление проводника в омах, длину проводника в метрах,

s— площадь поперечного сечения в квадратных миллиметрах, р — удельное сопротивление материала, то можно написать следующую формулу:

Эта формула показывает, что сопротивление проводника Rувеличивается с увеличением его длины l и уменьшается с увеличением площади S поперечного сечения.

Из приведенной выше таблицы видно, что наименьшим удельным сопротивлением, а следовательно и наилучшей проводимостью, обладает серебро. Однако оно очень дорого, а потому и не находит себе применения на практике. Следующим металлом с хорошей электрической проводимостью, мало уступающей серебру, является медь, которая и нашла себе применение в качестве материала для электрических проводов. Продажная медь содержит в себе железа, мышьяка и других примесей, которые уменьшают ее электрическуюпроводимость. Поэтому производят очистку меди электролитическим путем. Удельная проводимость электролитически очищенной меди достигает 97% химически чистой меди, и такая медь называется¹ проводниковой медью. В качестве проводникового материала применяют также алюминий и железо (телеграфная проволока).

Сплавы из нескольких металлов обладают большим удельным сопротивлением, чем чистые металлы. Как видно из таблицы (стр. 6O),^V сплавы нейзильбер (цинк, медь и никель), манганин (марганец, медь и никель), никкелин и нихром (хромоникель) обладает очень большим удельным сопротивлением, которое для нейзильбера в 12 раз, а для хромоннккеля в 57 раз больше, чем для меди. Поэтому означенные сплавы применяются в тех приборах, которые должны обладать большим сопротивлением, например в различных грелках и кипятильниках.

Жидкости тоже оказывают сопротивление проходящему через них электрическому току, а потому в •таблицах часто дают удельное со­противление различных растворов. Однако, под удельным сопротивле­нием жидкостей понимают обыкновенно сопротивление 1 куб. см жидкости.

Пример 80. Найти сопротивление медной проволоки, длиною 570 м. и тол­щиною 2,26 мм.

Решение. Дано: i=570 м, d=2,26 мм, р=р.

Сначала! найдем поперечное сечение проволоки:         _ч   *

_f==*X<*' ₌ 3,14x 2,26 X 2,26 _{= 1} ^ ^
4               4   '

Сопротивление проволоки Rнайдем по формуле:

U — рХ _г —57Х ₄ — ₄ —А»".

Притер 31. Принята бухта проводника, диаметром проволоки 1,78 мм. Для определения ее длины омметром измеряли сопротивление всего проводника, и оно оказалось равным 4 омам.

Решение. Прежде всего по данному диаметру (толщине) проводника найдем его поперечное сечение:

_{< = !1}у₌3,14х1,7₈х1,78_==2|5^_юс-

Теперь будем рассуждать так: кусок медной проволоки, длиною 1 м и, поперечным сечением 1 кв. мм, обладает сопротивлением  ома. Если бы наша проволока, сопротивлением 4 ома, имела поперечное сечение 1 кв. мм, то она имела бы длину:   -

4:^ = 4 X 57 = 228м.

Однако, наша проволока имеет сечение не 1 кв. мм, а 2,5 кв. мм, а потому проводимость ее будет больше и для того чтобы получить сопротивление 4 ома, нужно взять не 228 м, а в 2,5 раза больше, а именно:

228 X 2,5 = 570

К точно такому выводу мы пришли бы, если бы воспользовались непосредственно приведенной выше формулой R= р х

Пример 32. Определить, из какого материала сделана проволока прибора, если ее длина  = 4 000 см, толщина (диаметр) равна 2,76 мм, а измеренное со­противление этой проволоки оказалось равным 3 омам.

Решение. Дано: l = 4000 см = 40 м; d = 2,76 мм, R = 3 Ом.

Для решения задачи следует найти удельное сопротивление R этого материала, т. е. нужно определить, какое бы проволока имела сопротивление, если бы ее длина была равна 1 м и площадь поперечного сечения была бы равна 1 мм.

Для этого, прежде всего, найдем площадь поперечного сечения нашей проволоки:

*X*₌3,UX 2,76*2,76

Теперь будем рассуждать так: если наша проволока, длиною 40 м, имеет сопротивление 3 ома, то сопротивление 1 м этой проволоки, сечением 6 кв. мм, должно быть в 40 раз меньше, а именно:

3:40 = 1 ома.

Однако эта проволока имеет поперечное сечение 6 кв. мм, и если бы это сечение было равно только 1 кв. мм, то сопротивление ее увеличилось бы в 6 раз, и было бы равно:

3     „    3X6   18   _л ., __Х 6=^ = 35 = 0,45 ома.

Таким образом, мы получили, что 1 метр нашей проволоки с площадью попе­речного сечения 1 кв. мм имел бы сопротивление 0,45 ома, а это есть не что иное, как удельное сопротивление материала, из которого сделана эта проволока. По таблице, помещенной на стр. 60, находим, что наиболее подходящим к этому числу материалом является манганин (сплав из меди, марганца и никеля).

§ 35. Зависимость сопротивления проводника от температуры.

Исследования показали, что сопротивление проводников при нагревании меняется, с повышением температуры сопротивление металлов увеличивается, а сопротивление жидкостей и угля уменьшается.

Увеличение сопротивления от нагревания происходит почти одина­ково для всех металлов (не сплавов). Увеличение сопротивления в омах, приходящееся на каждый ом сопротивления и на каждый градус Цельсия, называется температурным коэффициентом данного материала. Почти для всех металлов температурный коэффициент можно принять равным 0,004, и только для далее следует считать его несколько большим, а именно 0,0045.