Основы электротехники сильных токов. Электрические и магнитные явления, страница 18

Часто случается, что сопротивления приходится соединять между собой не последовательно, а параллельно, причем параллельным со­единением сопротивлений назы­вается такое соединение (рис. 87), при котором вместе соединяются

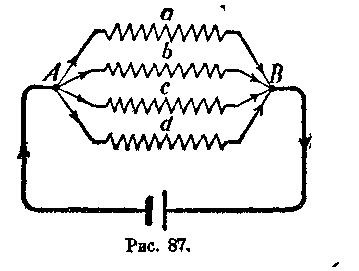
концы сопротивлений как с той, так и с другой стороны. При этом электрическому току приходится проходить по разветвленной цепи (рис, 87). В этом случае ток, выходя из положительного полюса эле­мента, доходит до узловой точки А; затем разветвляется по четырем па­раллельным ветвям а, Ь, с и d; в точке В все четыре тока сходятся вместе, и дальше общий ток возвращается к отрицательному полюсу элемент.

Так как сила тока определяется как количество электричества, про­ходящее в каждую секунду через поперечное сечение проводника, то но трудно понять, что сила тока в проводнике от элемента до раз­ветвления (до узловой точки А) равна силе тока в проводнике за разветвлением от узловой точки В до отрицательного зажима элемента.

Кроме того, сила тока в неразветвленной части равна сумме токов, проходящих по всем ветвям.

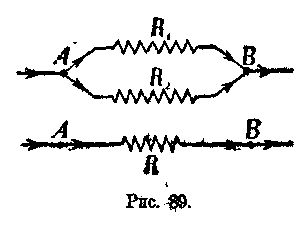
Для примера на рис. 88 изображены две электрических лампочки, соединенные между собой параллельно. В то время как при последовательном соединении сопротивлений общее сопротивление увеличивается, при параллельном соединении сопротивле­ний общее сопротивление уменьшается. Действительно, если мы по­смотрим на рис. 87, то увидим, что электри­ческий ток, дойдя до узловой точки А, имеет возможность идти несколькими путями (по ветвям) и при этом общее сопротивление, кото­рое он встречает на своем пути, будет меньше,  чем если бы он шел только по одной ветви. Возьмем разветвление, состоящее из двух ветвей R_tи R₂ (рис. 89). Это разветвление мы можем (мысленно) заменить одним сопротивле­нием, проводимость которого равна сумме проводимостей ветвей. Такое сопротивление В называется сопротивлением разветвления.

Итак, проводимость разветвления равна сумме проводимо­стей всех его ветвей.

Если же мы вспомним, что электрической проводимостью называется величина, обратная электрическому сопротивлению, то электрическая проводимость разветвления равна -п Поэтому для определения сопротивления разветвления мы имеем формулу: или, приводя к одному знаменателю дроби в правой части равенства:

' Отсюда для получения В нужно перевернуть дробь, и тогда получим:

B₁XB_i

Итак, в случае двух ветрей сопротивление разветвления равно произведению сопротивлений ветвей, деленному на их сумму. *

 

¹ Это правило является справедливым только для двух ветвей.

Пример 25. Найти сопротивление разветвления, состоящего из четырех ветвей, если сопротивление первой ветви равнб 4 омам, второй—5 омам, третьей— 10 омам и четвертой — 20 омам.

Решение.

Дано =4Q, B« — 5Q, R, = 10Qнй₄ = 20а.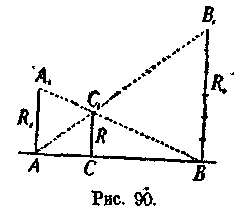

Электрическая проводимость разветвления равна сумме проводимостей ветвей

l-L+iA1 . 1_б + 4 + 2 + 1  .12

Сопротивление разветвления равно:

Предлагаем решить этог пример графическим путем, для чего сначала нужно найти сопротивление разветвления первых двух ветвей, а затем отдельно сопротивление разветвления третьей и четвертой .ветвей и, наконец, графическим путем, следует найти общее сопротивление всего разветвления.                      

Пример 26. Найти сопротивление разветвления, состоящего из двух ветвей если сопротивление одной ветви равно 20 омам, а сопротивление другой ветви в 9 раз меньше.

Решение..

Сопротивление другой ветви равно В_г = -^ Q.

Сопротивление разветвления:                                            '

20хД_1ХД₈__    ^Х 9 9_____________ 400

Ж+К ~~ ^ , 20 — 200 ~

Итак, если сопротивление прибора нужно уменьшить в 10 раз, то для этой цепи следует параллельно ему присоединить другое сопротивление, величина ко­торого составляет-g-сопротивления прибора. Такое сопротивление принято назы­вать шунтом, и говорят, что прибор зашунтован.

¹ Длину отрезка АВ следует выбрать .такой, чтобы линии A_tBи ABпо воз­можности пересекались бы под прямым углом. При соблюдении этого условия повышается точность графического построения.

§ .33. Законы разветвления тока.

Когда мы имеем дело с разветвлениями тока, то не трудно видеть, что в каждой узловой точке сумма токов входящих равна сумме токов входящих. Например, если в точке А (рис. ⁽Л) сходятся 4 тока, направления которые обозначены стрелками, то входящими токами будут токи /, и /₄ (стрелки  имеют направления к узловой точки), а уходящими токами будут /₃ и /₄ (стрелки направлены от узловой точки). Поэтому можно написать:

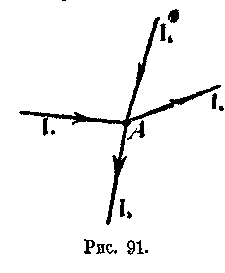h + h = h + h-

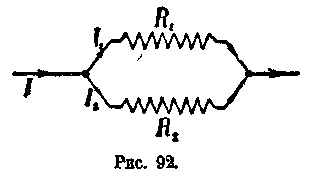
Пример 27. Имеем разветвление (рис 92), состоящее из двух ветвей Сила тока до разветвления измерена амперметром и оказалась равной 15 амперам. Сила тока  в одной ветви тоже измерена и равна 7 амперам. Определить силу тока во второй ветви.

Решение Дано: / = 15 A, /j = 7 А.

 Определить значение тока /,. Для узловой точки А имеем:

/ = Л f I, или 15 = 7 + 4 Отсюда ток /₃ = 15— 7 = 8 амперам.

Если разветвление состоит из двух совершенно одинаковых сопро­тивлений Л_г и Л_ъ то ток / от узловой точки (рис. 92) разделится на две равных части, т. е. сила тока в проводнике Л, будет равна силе тока в проводнике причем сила тока в проводнике до разветвле­ния, очевидно, будет в два раза больше, чем каждой из ветвей.

Если же сопротивления ветвей будут неодинаковы, т. е, если ветви обладают разными проводимостями, то, само собой разу­меется, ток будет сильнее в той ветви, которая обладает большой про­водимостью. Так, например, если сопротивление одной ветви в два раза больше сопротивления второй, то сила тока в проводнике с сопроти­влением Ii_tбудет в 2 раза меньше, чем в проводнике с сопротивлением  Д₂- Сила , тока в неразветвленной части цепи (до _/ точки А и после точки В) будет равна сумме токов, проходящих по обеим вет­вям.

Для определения силы тока в вет­вях, имеющих различное сопротивление, воспользуемся уже известным нам правилом для нахождения падения напряжения в проводниках. Напомним еще раз, что падение напряжения в какой-нибудь части цепи равно произведению из силы тика на сопротивление этой части цепи.