Математические методы теории принятия решений: Курс лекций, страница 52

Таблица 38

Сводные результаты решения задачи

На базе данных табл.38 можно решать и другие задачи распределения финансовых ресурсов. Например, при объеме финансирования  млн. ден.ед. для трех заводов максимальный объем прироста продукции составит  млн. ден.ед. Для этого понадобится распределить финансы только между двумя заводами: третьему - 40 млн. ден.ед. 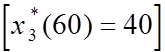, второму -
20 млн. ден.ед. 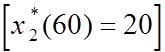, первому  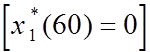- ничего выделять не надо.

Как видим, и в этом примере действует тот же алгоритм, какой будет справедливым и для рекуррентной формулы (8). Но содержательность (качественная сторона) информационных ресурсов, позволяющая на базе данных решать и другие задачи, очевидна.

Контрольные вопросы по теме №10

1.  В чем состоит главное отличие непрерывных и дискретных переменных в функциональных зависимостях?

2.  Каково необходимое условие существования экстремума?

3.  Каково достаточное условие существования экстремума?

4.  Является ли отсутствие ограничений в классическом математическом анализе недостатком?

5.  Каковы основные преимущества метода динамического программирования перед классическим математическим анализом?

6.  Для примера загрузки самолета вывести функциональную зависимость (8).

7.  Объяснить, почему на каждом шаге в примере загрузки самолета появляются ограничения типа 0 £ X_n £ P_с / P_n?

8.  Объяснить оправданность интерпретации числа предметов (загрузка самолета) числу шагов по объектам любой природы.

9.  В примере загрузки самолета, чем объяснить различие целочисленного и не целочисленного результатов моделирования?

10.  Чем различаются понятия: программа управления и синтез управления?

11.  В чем заключается существо решения задачи Коши?

12.  Назовите особенности применения МДП при решении задач с непрерывными переменными.

13.  Назовите особенности применения МДП при решении задач с дискретными переменными.

14.  Объясните алгоритм решения задачи распределения ресурсов для четырех заводов на базе МДП.

15.  В чем состоит содержательность (качество) информационных ресурсов, полученных при решении задачи для четырех заводов?

Приложение 1

Минимальное возрастание стоимости комплекса работ

На рис.16 изображена последовательность выполнения комплекса работ.

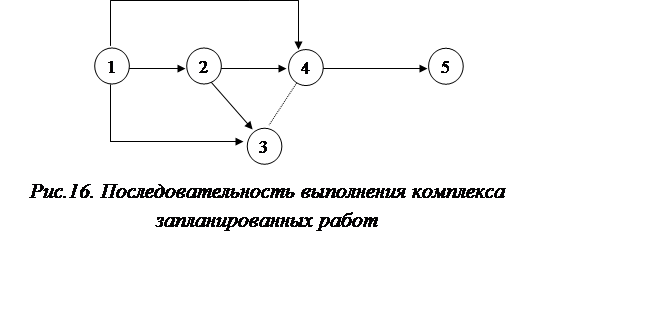Соответственно заданы минимальная и максимальная стоимость выполнения каждой работы: С_12,min = 150; С_12,max = 190; С_13,min = 111; С_13,max = 175;С_14,min = 30; С_14,max = 90; С_23,min = 66; С_23,max = 150; С_24,min = 72; С_24,max = 112; С_45,min = 89; С_45,max = 123. Кроме того, заданы коэффициенты дополнительных затрат, характеризующие увеличение стоимости работ при уменьшении их продолжительности
k_ij = (C_ij,max - C_ij,min) /(t_ij,min - t_ij,max) :

k₁₂ = 5; k₁₃ = 8; k₁₄ = 15; k₂₃ = 3; k₂₄ = 40; k₄₅ = 17.

Требуется минимизировать возрастание стоимости данного комплекса работ с тем, чтобы уменьшить первоначально заданные значения длительности работ табл.39.

Таблица 39