Это значит, что оптимальное значение нормы накопления b* равно коэффициенту эластичности замещения капитала a. Таким образом, норма накопления капитала b* связана с фактором экономического развития a, величиной инвестиций.
В модели Солоу заложены следующие 10 предпосылок:
1. Производственная функция: Y=F(K, L) (1)
Первые производные функции (1) больше нуля, вторые – меньше нуля. Символом Y обозначен результат функционирования экономического объекта (выпуск продукции, доход); K – размеры капитала; L – размеры трудовых ресурсов.
2. Величина выбытия капитала: W = d×K, (2)
где d - норма выбытия капитала.
3. Норма сбережений (инвестиций) b постоянна и поэтому количество инвестируемых единиц: I = b×Y (3)
4. Значение: Y = C + I, (4)
где С – величина потребления.
5. Производительность труда: y = Y/L (5)
6. Капиталовооруженность: x = K/L (6)
7. При делении обеих частей формулы (1) на L получим:
y = f(x) (7)
8. Размеры инвестиций характеризуют изменение величины капитала во времени: dK/dt = I, (8)
причем удельные (на единицу труда) инвестиции:
i=I/L (9)
9. Темп численности занятых на производстве n, трудосберегающий темп НТП (научно-технического прогресса) g и норма выбытия капитала d связывают величину удельных инвестиций и капиталовооруженности соотношением:
i = (d + n + g)×x (10)
10. Если формулу (4) записать для единицы трудового ресурса, то производительность труда будет: y = c + i, (11)
а удельные инвестиции: i =b×f(x) (12)
Значение капиталовооруженности x находится в устойчивом равновесии, если ее прирост за счет инвестиций компенсирует ее уменьшение за счет других факторов. Это положение отразим в (13):
(d + n + g)×x* ==b×f(x*), (13)
где x* - устойчивый уровень капиталовооруженности.
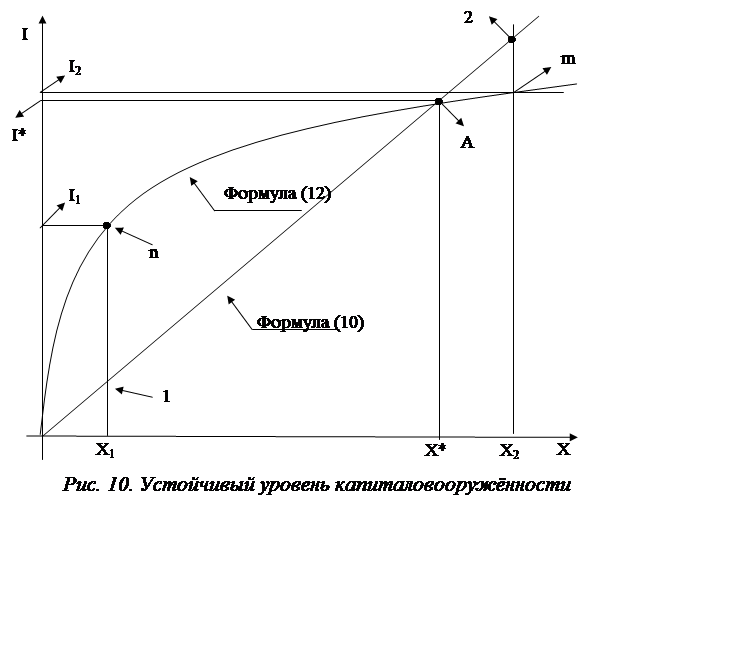 |
На рис.10 показана зависимость i = f(x).
В точке А удельный прирост x точно равен величине его удельного сокращения и поэтому xA = x*. Это равновесие устойчиво, так как при x1 < x* инвестиции i1 (точка n) превышают их величину (точка 1), подсчитанную по формуле (10). При x2 > x* инвестиции i2 (точка m) ниже их значений в точке 2. Значение инвестиций в точке А, равное величине i* = (d + n + g)×x*, соответствует устойчивому значению капиталовооруженности x*.
Рассмотрим следующие состояния развивающейся экономики.
1. С ростом b происходит рост инвестиций (формула (12)). Тогда функция инвестиций пересечет прямую линию (d + n + g)×x – правее. Значит, рост b увеличивает устойчивый уровень x*. Благосостояние населения при этом улучшается.
2. Если численность работающих не увеличивается (n=0), то прямая линия (d + n + g)×x будет иметь меньший наклон к горизонтальной оси и, значит, точка x* сдвинется вправо. (То же будет и при g = 0).
3. Темпы прироста y, x, c, i в устойчивом состоянии экономики равны нулю. Поэтому, если g > 0 (темп НТП), эти величины также будут расти.
4. При росте темпа n численности занятых на производстве общий объем капитала, дохода, потребления и инвестиций возрастают с темпом (n+g). Это значит, что надежным источником длительного и устойчивого роста благосостояния населения является научно – технический прогресс [6].
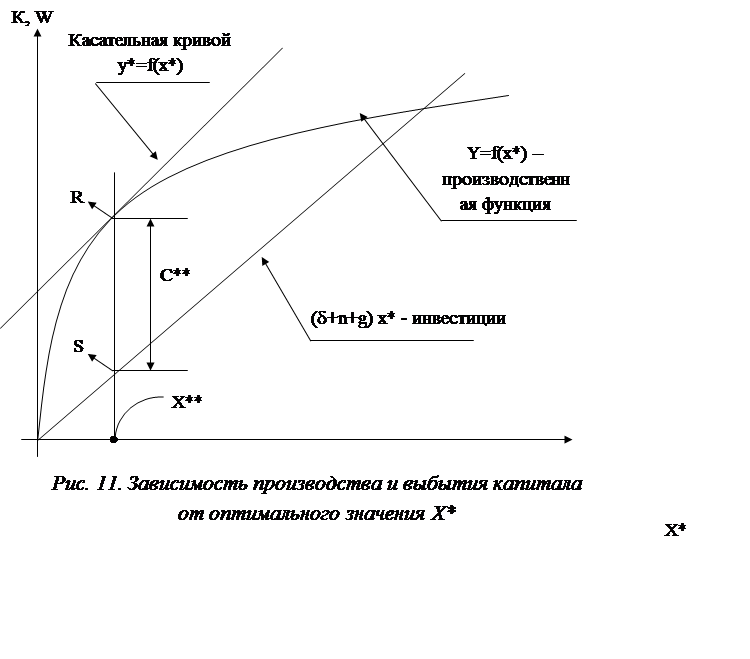
Поскольку каждому уровню нормы сбережения b отвечает определенное устойчивое состояние и уровень удельного потребления с*, возникает вопрос, при каких условиях значение с* будет максимальным?
Используя формулу (10) и (11), получим:
с* = y*- i* = f(x*) – (d + n + g)×x* (14)
Равенство нулю правой части, после взятия первой производной в формуле (14), дает:
d[f(x*)] = (d + n + g) (15)
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.