Для каждой модели следует сделать выводы по результатам расчета так, как мы уже неоднократно это делали в других задачах. Поскольку рассмотренные четыре линейные задачи характеризуют деятельность системы отраслей, полученные значения информационных ресурсов позволяют принять обоснованные управленческие решения.
Сопоставление статического и динамического МОБ показывает, что первые два квадранта динамического МОБ выглядят (табл.10):
Таблица 10
Сопоставление статического и динамического МОБ
|
Отрасли |
Межотраслевые потоки текущих затрат |
Прирост ОПФ |
Конечный продукт |
Валовый продукт |
||||
|
j=1 |
j=2 |
j=n |
j=1 |
j=2 |
j=n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выводы:
1. Матрица текущих затрат динамического МОБ совпадает с матрицей статического МОБ.
2.
Элементы матрицы ![]() показывают количество
показывают количество ![]() -того продукта, направленного в текущем
периоде в
-того продукта, направленного в текущем
периоде в ![]() -тую отрасль в виде капиталовложений в ее
ОПФ (характеристика прироста запасов сырья, материалов, оборудования, площадей,
транспорта и т.п.).
-тую отрасль в виде капиталовложений в ее
ОПФ (характеристика прироста запасов сырья, материалов, оборудования, площадей,
транспорта и т.п.).
3.
В статическом МОБ поток вложений не дифференцируется по
отраслям-потребителям (дается общая величина ![]() ). В
динамическом МОБ конечный продукт включает продукцию
). В
динамическом МОБ конечный продукт включает продукцию ![]() -той
отрасли, идущую в личное
-той
отрасли, идущую в личное ![]() и общественное
и общественное ![]() потребление.
потребление.
4.
Сумма потоков ОПФ и конечного продукта в динамическом МОБ ![]() равна величине
равна величине ![]() :
:
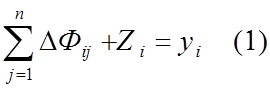 и
и 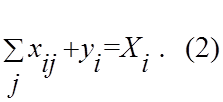
5. Распределение продукции отраслей в динамическом МОБ следует уравнению:
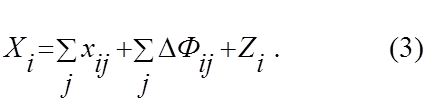
6.
Прирост производственной продукции по времени ![]() :
:
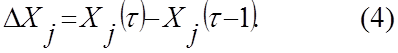
В уравнении (4) предполагается, что прирост продукции эквивалентен
приросту ОПФ, т.е. ![]() , где
, где ![]() - коэффициенты капиталовложений,
показывающие, сколько продукции
- коэффициенты капиталовложений,
показывающие, сколько продукции ![]() -той отрасли надо
вложить в
-той отрасли надо
вложить в ![]() -ю отрасль для увеличения мощности последней,
чтобы расширить выпуск продукции на одну единицу (капиталоемкость единицы прироста
выпуска).
-ю отрасль для увеличения мощности последней,
чтобы расширить выпуск продукции на одну единицу (капиталоемкость единицы прироста
выпуска).
7. Теперь с учетом (4) выражение (3) можно дать в виде линейного разностного уравнения 1-го порядка:
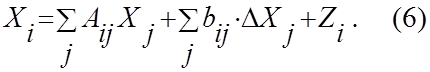
8.
Считая, что все объемы производства и конечной продукции относятся к
периоду ![]() , а прирост определяется в сравнении с периодом
, а прирост определяется в сравнении с периодом
![]() , получим:
, получим:
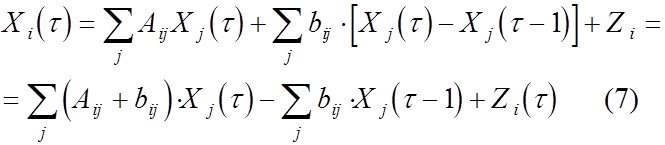
При заданных ![]() и
и ![]() выражение (7) – обычная система n линейных уравнений с
выражение (7) – обычная система n линейных уравнений с ![]() -неизвестными.
-неизвестными.
Динамические модели МОБ представляют большую ценность для
управления экономическими системами, в том числе – для развития
экономических объектов. Эти модели можно разделить на
2 группы: не оптимизационные и оптимизационные модели.
Весьма важными являются две оптимизационные задачи [4]:
1. накопления капитала (одного из агрегированных ресурсов производственных функций);
2. потребления с учетом ограниченного использования труда (второго агрегированного ресурса производственных функций).
Введем следующие обозначения:
·
![]() -
вектор оценки запасов ресурсов в последнем этапе временного периода;
-
вектор оценки запасов ресурсов в последнем этапе временного периода;
·
![]() -
матрица коэффициентов капиталоемкости (коэффициенты
-
матрица коэффициентов капиталоемкости (коэффициенты ![]() );
);
·
![]() -
матрица коэффициентов прямых затрат (коэффициенты
-
матрица коэффициентов прямых затрат (коэффициенты ![]() );
);
·
![]() -
матрица коэффициентов роста затрат;
-
матрица коэффициентов роста затрат;
·
![]() -
единичная матрица;
-
единичная матрица;
·
![]() -
соответственно отыскиваемые значения оптимальных объемов выпуска и в первоначальный
период;
-
соответственно отыскиваемые значения оптимальных объемов выпуска и в первоначальный
период;
·
![]() - рассматриваемый временной
период оптимизации.
- рассматриваемый временной
период оптимизации.
В исходные данные также включаются: ![]() - число отраслей промышленности;
- число отраслей промышленности; ![]() -
количество формул-ограничений;
-
количество формул-ограничений; ![]() -число основных переменных; коэффициенты состояния активов: основных
фондов, товарных запасов, амортизации основного капитала.
-число основных переменных; коэффициенты состояния активов: основных
фондов, товарных запасов, амортизации основного капитала.
Тогда целевая функция – максимизация суммы накопленного капитала за рассматриваемый период – будет (в векторной форме):
![]()
Ограничения:
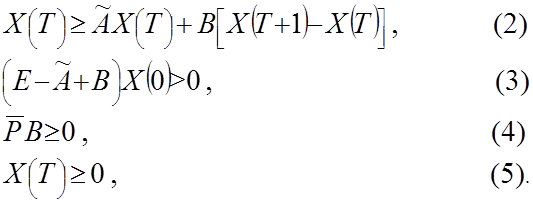
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.