Математические методы теории принятия решений: Курс лекций, страница 5

1).   и ;

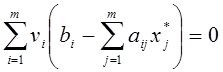2).   и ;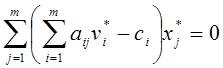

3).  Для всякого , если , то 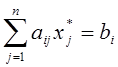; для всякого , если , то .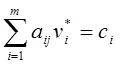

Сущность второй теоремы: если двойственные оценки положительны, то есть V_i* > 0, то ресурсы дефицитны (т.е. они полностью использованы, а их неиспользуемость S_i = 0). Если же V*_i = 0, то ресурсы находятся в избытке и потому значение S_i > 0.

Третья теорема двойственности. Значения переменных V*_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов  системы ограничений прямой задачи на величину .

Третья теорема двойственности доказывается так:

Df(x) = V*_i×Db_i

Если Db_i = 1, то |Df(x)| = |V_i*|. То есть, изменение значения целевой функции при изменении соответствующего ресурса на единицу составит столько единиц, сколько их в положительных оценках V_i*.

Правила формулировки двойственной задачи на основе прямой задачи:

1. Количество неизвестных в двойственной задаче равно числу функциональных ограничений в прямой задаче.

2. Экстремум целевой функции двойственной задачи формулируется противоположным по смыслу прямой задачи: вместо максимума - минимум (а вместо минимума - максимум).

3. Число ограничений в системе двойственной задачи равно числу переменных в исходной задаче.

4. Правыми частями в ограничениях двойственной задачи являются коэффициенты при неизвестных в целевой функции прямой задачи.

Теперь сформулируем модель двойственной задачи:

Информационные ресурсы результатов решения можно свести в следующую таблицу:

Таблица 1

Рассмотрим интерпретацию трех теорем двойственности, сформулированных выше.

Первая теорема двойственности

Вторая теорема двойственности

Если   . Значит, 1-й и 2-й ресурсы будут находиться в дефиците.

Значения   . Значит, 3-й и 4-й ресурсы будут находиться в избытке.

Третья теорема двойственности

Изменим значение 1-го ресурса на единицу, т.е.  и тогда .

Тогда  денежных единиц.

Разница  ден.ед. - т.е. это составляет столько единиц, сколько их в двойственной оценке 1-го ресурса  денежных единиц/ед. ресурсов.

Если , то  ден.ед., т.е.  ден.ед. ().

Нужно отметить, что в случае заявки на производство новой продукции, экономическая целесообразность устанавливается по критерию :

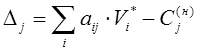
Если , производство новой продукции экономически оправдано (для нашего оптимального решения ).

Если , то производство новой продукции экономически нецелесообразно.

При решении оптимизационных задач переменные могут оказаться дискретными: целочисленными, булевыми и дробными.

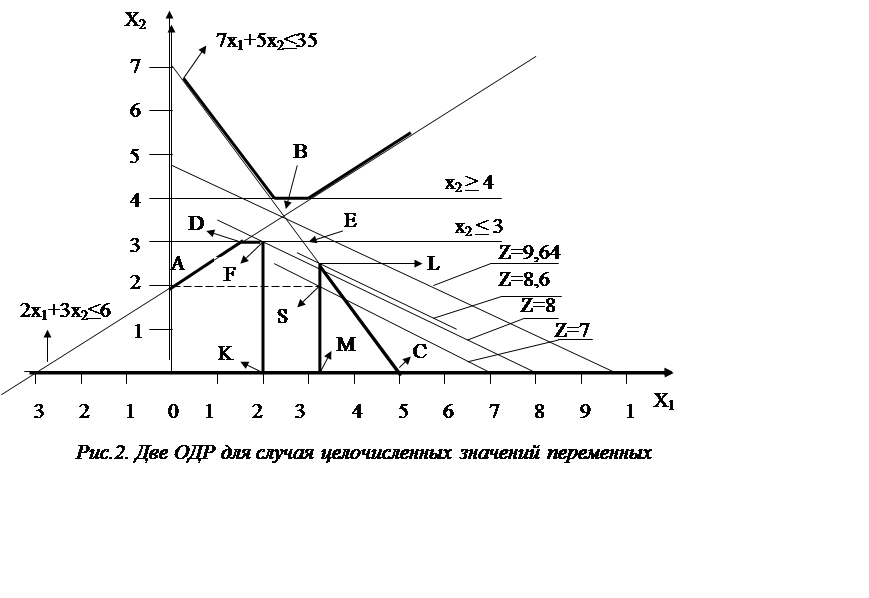
В случае целочисленных переменных область допустимых решений может состоять из нескольких разрозненных областей. Ниже приводится пример, когда условие целочисленности для исходной задачи №1 приводит к появлению задач №2 и №3 (в задаче №3 ОДР оказывается пустой). Тогда задача №2 распадается еще на две задачи: №4 и №5. Задача №5 распадается еще на две: №6 (ОДР – пустая) и №7. В задаче №4 получено целочисленное решение с большим значением целевой функции, чем в задаче №7 – то же с целочисленным результатом. Вывод ясен: решение заключено в варианте задачи №4. Приведем этот пример.

Найти максимальное значение целевой функции Z= x₁ + 2x₂ при ограничениях:

7x₁ + 5x₂ £ 35            (1)

-2x₁ + 3x₂ £ 6           (2)

Значения переменных должны быть неотрицательными и в целых числах. Решение задачи №1: Z = 9,64; x₁=2,42; x₂ =3,61. На
рис.2 – это координата точки В. Целочисленный результат переменных не достигнут.

		Рис. 2. Две ОДР для случая целочисленных значений переменных