Математические методы теории принятия решений: Курс лекций, страница 22

x*₁ = S₁(P_o, p₁, p₂), x*₂= S₂(P_o, p₁, p₂)         (12)

Соответственно, функция предложения на выпускаемую продукцию запишется в виде соотношения:

у*=F[S₁(P_o, p₁, p₂), S₂(P_o, p₁, p₂)]                (13)

Функции спроса на ресурсы для краткосрочного периода

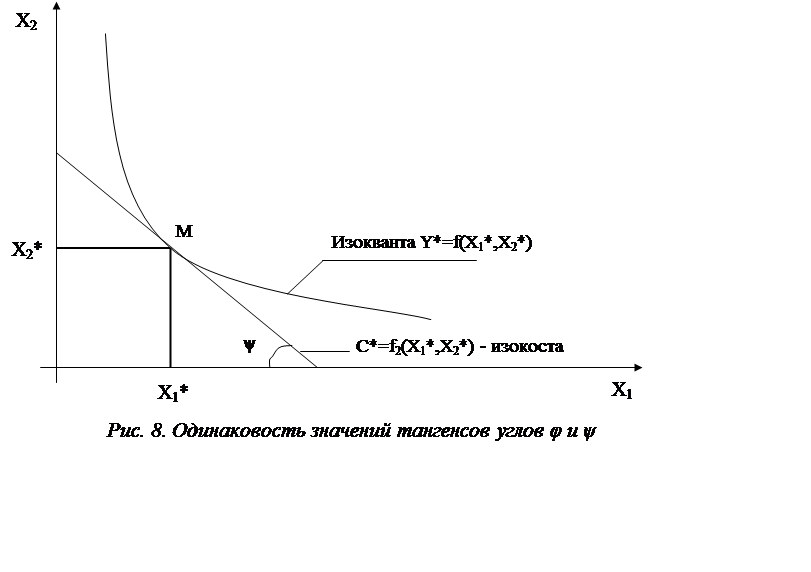
Эта ситуация характерна при наличии ограничения на ресурсы. Пусть ограничен (его значение отмечено верхним индексом «ф») второй ресурс x₂^ф.

Пусть его значение находится в диапазоне:

x₂^* > x₂^ф > 0                                (14)

Тогда целевая функция максимизации прибыли запишется в виде:

PR(x₁, x₂^ф) = P_o×f(x₁, x₂^ф ) – (р₁× x₁ + р₂× x₂^ф)®max    (15)

Приравнивая к нулю первую производную, получим:

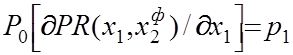                  (16)

На рис.9 в точке В(x₁^ф, x₂^ф) показано выполнение условия (14). В этой точке локального равновесия изокванта(заданные объемы выпускаемой продукции) и изокоста 2-2 уже не касаются, а пересекаются. Изокоста 2-2, проведенная через точку В, имеет большее значение производственных издержек, чем параллельная ей изокоста 1-1. Только в точке А с координатами x₁^*, x₂^* находится глобальный минимум издержек производства. Именно точка А(x₁^*, x₂^*) обеспечивает минимум издержек производства при заданном объеме выпуска продукции.

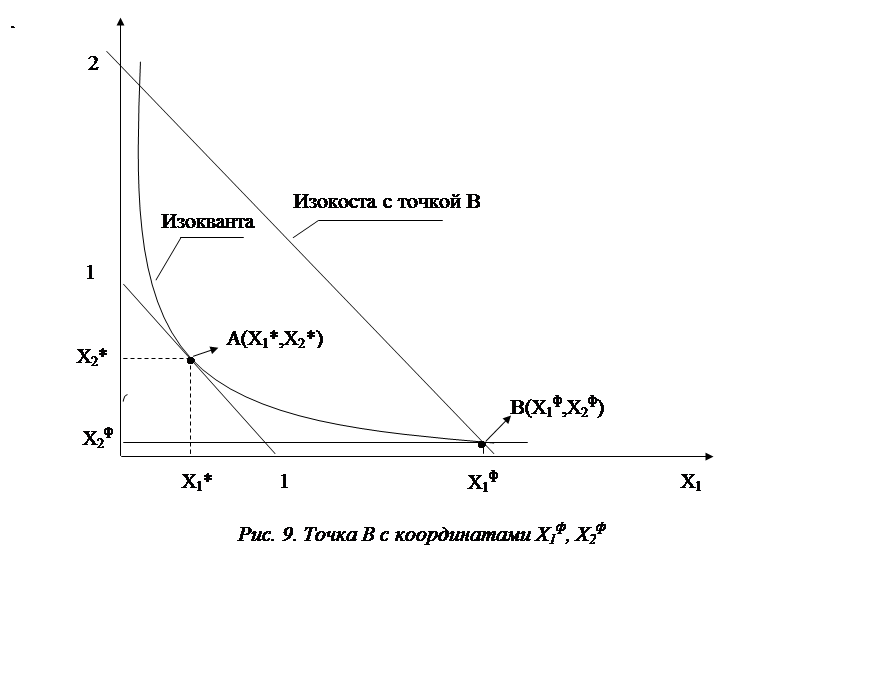
Горизонтальная линия Х₂^ф – В на рис.9 называется линией краткосрочного развития производства.

Аналогично предыдущему параграфу запишем функцию спроса на первый ресурс (при фиксированном значении второго):

x^ф₁= F₁(x^ф₂, P_o, p₁, p₂)                                  (17)

Тогда функция предложения на выпуск продукции будет:

Y = F₂(x^ф₂,P_o,p₁,p₂)                             (19).

Динамическая модель оптимального размещения выпускаемой продукции по отраслям промышленного производства (производственно – транспортная модель)

Обозначим продолжительность всего планового периода через Т, лет, а текущее значение промежутка времени t, единиц времени. Индексы предприятий и потребителей, соответственно, будут обозначены i и j; значения этих индексов: i = 1, n; j = 1, m. Тогда для производства: X_it – объем валового выпуска продукции на i – том предприятии в t – ом периоде, единиц продукции; Q_it – затраты на производство единицы продукции на i – том предприятии в t – ом периоде, ден. единиц / ед. продукции; A_it – максимальная мощность
i – го предприятия в t – ом периоде, единиц продукции.

Для потребления:

·  X_ijt – объем перевозок продукции из i – го предприятия к
j – му потребителю в t – ом периоде;

·  C_ijt – тариф перевозок продукции из i – го предприятия к
j – му потребителю в t – ом периоде, ден. ед. / ед. продукции;

·  B_jt – объем поставок продукции j – му потребителю в t – ом периоде, единиц продукции.

1. Целевая функция - необходимость разместить производство продукции по предприятиям так, чтобы за время планового периода Т суммарные затраты были минимальными – записывается в виде:

Z = S_tS_i Q_it× X_it + S_tS_iS_j C_ijt× X_ijt ® max                  (1)

2. Условия производства продукции:

X_it < = A_it, а поскольку X_it = S_j X_ijt, то

S_j X_ijt< = A_it                                                      (2)

3. Условия потребления продукции:

S_i X_ijt = B_jt                                                        (3)

4.Условия производственного роста:

X_i,t+1 > X_it      ,                                                  (4)

где значения индекса i – прежние, а индекса t = 1, T – 1.

5. Условия неотрицательности переменных:

X_it = > 0;

X_i,t+1 = > 0;                                                        (5)

X_ijt = > 0

Здесь укажем на важность только нескольких этапов информационной технологии моделирования по этой задаче.

Объект моделирования. Любая планируемая, реконструируемая или существующая социально – экономическая система.

Проблемная ситуация. Поиск минимума совокупных затрат на развитие социально – экономической системы с учетом указанных выше условий производства, потребления и экономического роста.

Математический аппарат. Линейная алгебра. Вследствие линейности динамической модели – богатство информационных ресурсов (см. материал темы 1).