где l - множитель Лагранжа. Безусловный экстремум этой функции совпадает с условным экстремумом только для точек, удовлетворяющих приведенному условию j(x1, x2) = b. Только тогда второе слагаемое функции Лагранжа обращается в нуль. Для остальных точек L(x1, x2, l) ¹ f(x1, x2).
Если y, Po – соответственно, общий объем выпуска продукции и ее рыночная цена, то величина дохода будет выражена записью:
R = y× Po (1)
При известных ценах р1, р2 и объемах затраченных ресурсов x1, x2 издержки производства составят:
С = р1× x1 + р2× x2 (2)
Величина прибыли – разность дохода и издержек:
Z = R – C = Po×f(x1, x2) – (р1× x1 + р2× x2) (3)
Значения объемов ресурсов – неотрицательны. Задача максимизации прибыли в терминах стоимости ресурсов имеет вид:
Z=F(x1,x2)®max (4)
Если дополнительные ограничения на ресурсы отсутствуют (что соответствует долгосрочному периоду D), то это задача безусловной оптимизации решается через метод неопределенных множителей функции Лагранжа. Если на объемы используемых ресурсов заданы ограничения типа:
g(x1, x2) £ b (5),
то оптимизация называется условной.
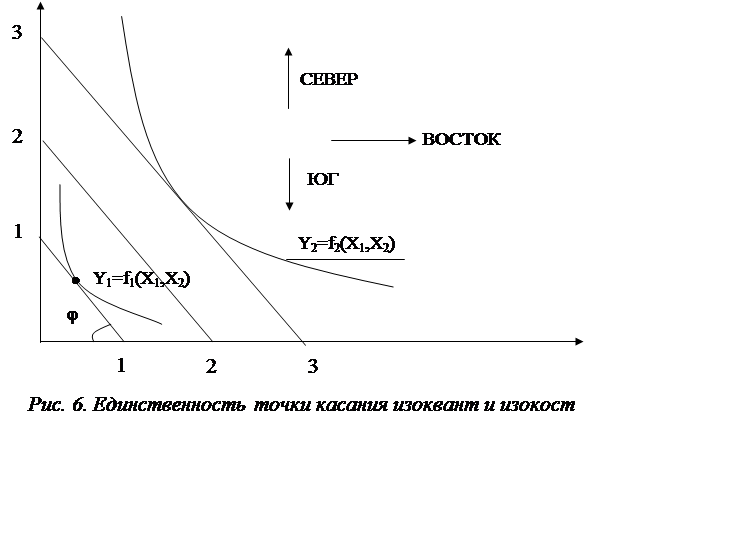
Прямые линии правой части соотношения (2) называются изокостами.
Чем «северо-восточнее» относительно изокосты 1-1 располагаются эти линии, тем
больше стоимость затраченных ресурсов – рис.6. На рис.6 видно, что тангенс угла
наклона прямой (tg j), касательной к кривой
постоянного объема выпуска (изокванты), определяет единственную точку
касания. Значение объемов выпуска
у2 > у1:
вместе с ростом объемов выпуска растут и издержки производства.
 |
Для целевой функции – максимизации прибыли:
Z = R – C = Po×f(x1, x2) – (р1× x1 + р2× x2) ® max,
ограничения на ресурсы не указаны.
Значит, это задача на глобальный экстремум, для точек которого
справедливы соотношения
¶z/¶x1 = 0; ¶z/¶x2 = 0
или
Po× ¶z/¶x1 = р1; Po× ¶z/¶x2 = р2 (6)
При отрицательных значениях вторых частных производных,
изображение производственной функции у = f(x1,
x2) в трехмерном пространстве – поверхность, выпуклая вверх
(типа «колокол»). Верхняя точка «колокола» соответствует глобальному
максимуму прибыли. Это означает, что система (6) имеет единственное
решение с координатами x*1, x*2. Вектор затрат
ресурсов x*1, x*2 называется локальным рыночным
равновесием для конкретного производст-
ва [6].
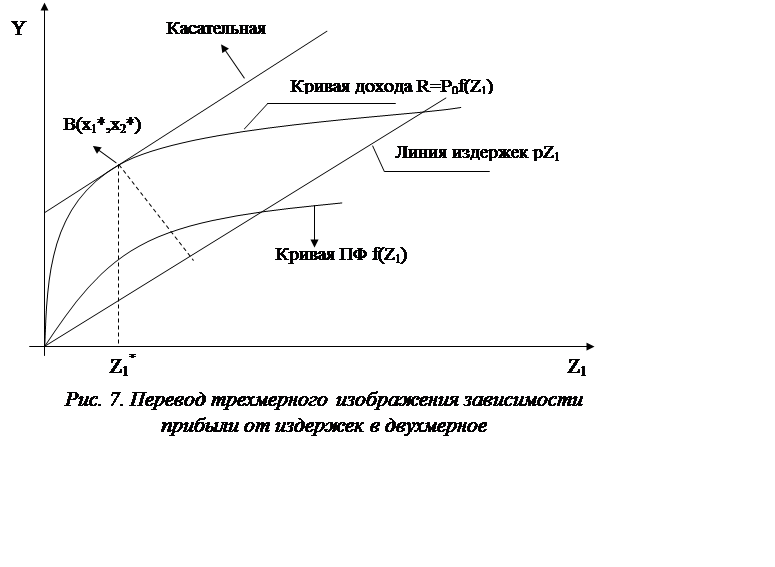
Если график трехмерного изображения перевести в двумерное (тогда плоскость Оx1, x2 станет горизонтальной осью Оz1 на рис.7), то можно построить производственную функцию у = f(z1); функции дохода у = Po×f(z1) и стоимости издержек производства С = р×z1. Тогда значения прибыли получаются, как разность значений графика дохода и издержек PR = Po×f(z1) - р×z1 (7). В точке В с координатами x*1, x*2 находится максимум прибыли.
Подставив значения x*1, x*2 в уравнение (6), получим:
Po× ¶z*/¶x*1 = р1; Po× ¶z*/¶x*2 = р2 (8)
По членное деление слагаемых (8) дает:
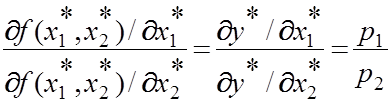 (9)
(9)
Это значит, что в точке x*1,x*2 рыночного равновесия отношение предельных производительностей первого и второго ресурсов равно отношению их рыночных цен.
 |
На рис.8 показана изокванта у* = f(x*1, x*2). Поскольку связь между переменными x1, x2 можно выразить: x2 = h(x1), то получим следующее соотношение:
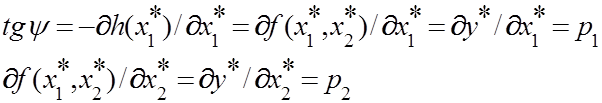 (10)
(10)
Из математического анализа следует, что для касательной (прямой, касающейся изокванты в точке М(x*1, x*2)),отношение:
р1/р2 = tgy (11)
Поэтому из (9), (10), (11) следует, что значение tgy = tgj. Точка касания М(x*1, x*2) появилась лишь тогда, когда была решена система (8). Это значит, что изокоста на рис.6 совпала с касательной на рис.8. Факт касания – доказательство существования экономического равновесия, при котором обеспечивается наилучшие значения расходуемых ресурсов для заданного объема выпускаемой продукции. Конечно, значения x*1, x*2 зависят от цен на ресурсы. Это отражается в функциях спроса на ресурсы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.