Математические методы теории принятия решений: Курс лекций, страница 25

На рис.11 приведены соответствующие зависимости в координатах: K, W – производство и выбытие капитала, соответственно (вертикальная ось); значения x* - горизонтальная ось. Рис.11 показывает, как выбирается оптимальный объем капитала при максимизации с* по «золотому правилу экономики». Этому правилу будут соответствовать значения x** и b*. Значение b* определяется из уравнения устойчивого состояния экономики:

(d + n + g)×x** = b*×f(x**)                                (16)

Тогда и величина удельного потребления с** «по золотому правилу» будет представлять разность:

с** = y** - i** = f(x**) - (d + n + g)×x            (17)

Отсюда вытекают три характерные ситуации:

1.Если темп роста трудовых ресурсов n более низок, чем первоначальный, то точка x** сдвинется вправо, а значение с** увеличится.

2. Если первоначальное значение x*< x**, то увеличивают норму сбережения b до значения «по золотому правилу». Тогда экономика постепенно выходит на максимальный уровень с** - рис.12а. В начале удельный уровень потребления будет даже несколько ниже исходного и, лишь затем, постепенно вырастет наряду с ростом инвестиций i и производительности труда у.

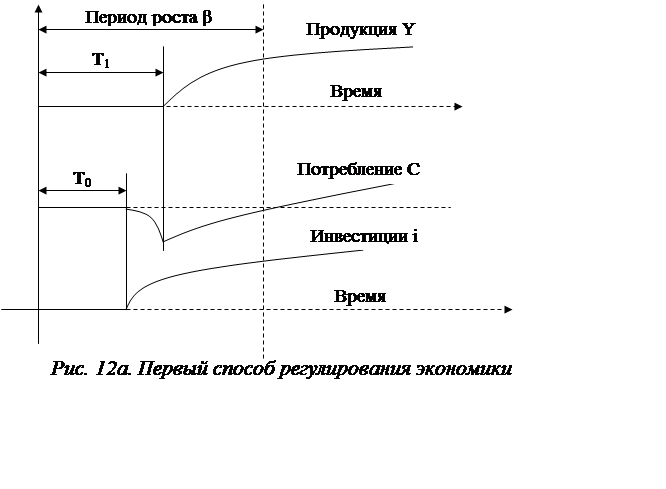3. Если же x*>x**, то снижают значение b (норму сбережений) до уровня, соответствующему «золотому правилу». Тогда экономика постепенно выходит на требуемый уровень с**. Причем, вначале удельное потребление даже несколько вырастет, а затем будет постепенно снижаться наряду со снижением инвестиций i и производительности труда, которые первоначально имели более высокие значения – рис.12б.

Математические основы теории трудовой стоимости

Модель продаж и рынка одного товара

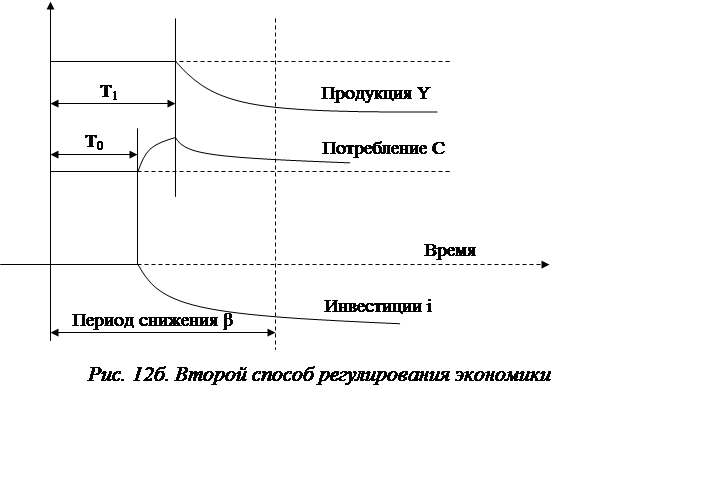На рис.13 изображена зависимость спроса D(p) и предложения S(p) от цены товара р. В точке равновесия M(S*,D*) спрос точно соответствует предложению. Пусть зависимость спроса от цены подчиняется линейной формуле:

D = 10 – p                                  (1)

Зависимость предложения от цены: S = 2 + p/4                 (2)

Из (1) следует, что цена зависит от спроса:

p = 10 – D                                   (3)

С учетом (2) зависимость цены от предложения:

p = 4S – 8 (4)

Значение цены, при котором S* = D*, равно p* = 6,4.

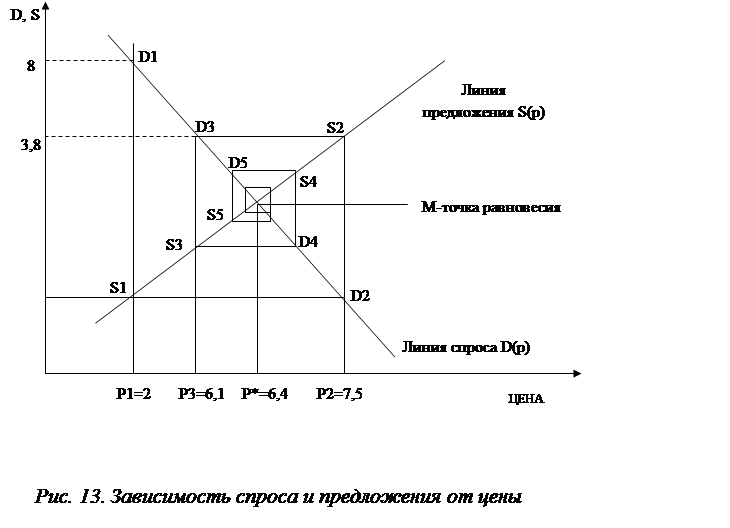
Рассмотрим эту ситуацию подробнее. При р₁ = 2 значение D₁>S₁. Это означает, что цену надо увеличить до значения р₂ = 7,5 и тогда
S₁ = D₂. Теперь продавцы определяют значение S₂ = 2 + 7,5/4 = 31/8, что больше величины спроса D₂. Это вызовет уменьшение цены до
р₃ = 49/8, в то время как прежнее значение было р₂ = 7,5. И только в точке M(S*,D*) обеспечивается значение равновесной цены p* = 6,4.

Модель производства множества товаров

Укажем на два конкретных обстоятельства, которые будут учитываться при последующем рассмотрении данного вопроса:

1.  Каждая отрасль может произвести любой объем продукции, если для этого объема будет достаточно ресурсов;

2.  Если продукция производится на внешнее потребление в количестве Y конечного продукта, то:

Y = X – AX   или   Y = X(E – A)              (5)

Окончательно получим: X = (E – A)^-1×Y = BY          (6)

В уравнении (6) значение А – заданная матрица ресурсов. Возникает вопрос, каким количеством ресурсов надо располагать, чтобы производить любое вещественное значение Y ³ 0 ? Ответ на этот вопрос: только, когда соблюдается условие:

(E – A)^-1 ³ 0                                               (7)

Тогда матрица А отражает способность к производству продукции, то есть она продуктивна.

Для непроизводственной сферы Y = X – AX = X(E – A) (8). Но на производство Y надо израсходовать AX ресурсов, а на производство этих AX ресурсов надо затратить A(AX) = A² ×X ресурсов. А на производство A² ×X ресурсов надо затратить еще А(A²×X) ресурсов и т.д. Сумма такого бесконечного ряда и есть полные затраты ресурсов. Поскольку в производственную функцию входит второй агрегированный ресурс L (трудовые резервы), очень важен вопрос, из каких условий надо определять его численное значение.