Математические методы теории принятия решений: Курс лекций, страница 46

Таким образом, теория нечетких множеств позволяет описывать состояния экономических явлений, которые могут не поддаваться непосредственным измерениям.

Теория нечетких множеств дает точное определение нечеткого числа, как подмножества действительных чисел универсального множества, обладающего свойствами нормальности и выпуклости функции принадлежности.

Основной особенностью применения нечетких множеств является однозначность факта принадлежности (не принадлежности) множеству. Использование ключевых понятий теории множеств (пересечение, объединение, дизъюнкция, дополнение) помогает с достаточной степенью достоверности установить факт принадлежности элемента рассматриваемому множеству.

Термин "оценка" в теории нечетких множеств имеет тот же смысл, что и математическое ожидание в теории вероятностей. Теория нечетких множеств рассматривает интервалы достоверности при всех уровнях достоверности от 0 до 1. В теории нечетких множеств применяются нечеткие треугольные числа (НТЧ). Укажем на следующие области применения НТЧ:

1.  Кратковременное и долгосрочное планирование процессов экономического развития;

2.  Управление запасами;

3.  Замена оборудования;

4.  Привлечение инвестиций;

5.  Отбор персонала;

6.  Управление качеством выпускаемой продукции;

7.  Многокритериальные оптимизационные задачи.

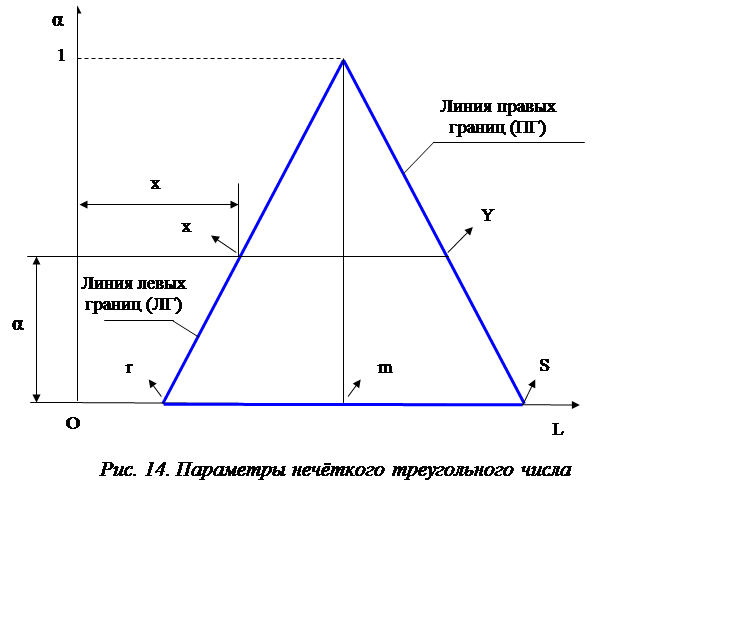
На рис.14 НТЧ показано в координатах: уровень достоверности (a) - интервал достоверности (L).

Все текущие значения левых границ интервала X и правых границ Y находятся из подобия соответствующих треугольников - рис.14. Из этого подобия следует:

(m - r)/(X - r) = 1/a                   (1)

Тогда текущие значения X и Y можно вычислить:

X = r + a×(m - r)

Y = s - a×(s - m)                       (2)

Приведем пример для расчета чистой приведенной стоимости NPV инвестиций. Проект характеризуется следующими размерами денежных средств, распределенных по периодам времени (t=0,1,2,3):

Для промежутков времени t=1, 3 известны значения НТЧ уровня доходности инвестиций (процентной ставки):

t=1:           (r1, m1, s1) = (8, 10, 13)

t=2:           (r2, m2, s2) = (9, 12, 15)

t=3:           (r3, m3, s3) = (7, 10, 12)

По формулам (2) рассчитаны интервалы достоверности процентов каждого года:

[r1, s1] = [8 + 2×a, 13 - 3×a]

[r2, s2] = [9 + 3×a, 15 - 3×a]

[r3, s3] = [7 + 3×a, 12 - 2×a]

При изучении материалов в темах 6 – 8 была приведена формула для расчета чистой приведенной стоимости:

NPV = - I_o +SF(t)×                        (3),

где I_o = 7000 д. ед. - инвестиции на нулевой момент времени.

Значение функции финансовых средств F(t) = 5000, 4000, 2000 денежных единиц для каждого последующего момента времени.

Все вычисления проводятся в следующей последовательности.

1. Момент времени t=1.

Коэффициент дисконтирования есть дробь: .

а) Сначала найдем сумму 1 + k.

Операция сложения нечетких чисел следует правилу:

[a, b] (+) [c, d] = [a +c, b + d].

Поскольку для единицы a = 1, b = 1, а для нечеткого числа k левая граница (ЛГ) интервала c = r, правая граница (ПГ) d = s, то сумма:

1 + k = [1 + r, 1 + s]

Для следующего шага значение левой границы будет c=1+r, а значение правой границы: d=1+s.

б) Теперь найдем частное .

Операция деления нечетких чисел следует правилу:

[a, b] (:) [c, d] = [a/d, b/c]

Тогда  = , и значения, соответственно, левых и правых границ составят: a = , b =

Теперь переходим к моменту времени t = 2.

2. Момент времени t=2.

Требуется найти коэффициент дисконтирования []².

Значение []² = []·[]

В правой части первый сомножитель относится к моменту времени t = 1, второй - к моменту времени t=2.

Операция умножения нечетких чисел следует правилу:

[a, b] (·) [c, d] = [a·c, b·d].

Это значит, что перемножаются значения левых границ для моментов времени, соответственно, t=1 и t=2, образуя значение левой границы интервала на момент времени t=2. Аналогично получается и результат значения правой границы для момента времени t=2.