Математические методы теории принятия решений: Курс лекций, страница 48

11.  Покажите, как используется основная формула (смотрите вопрос 10) при вычислении уровня доходности инвестиций.

12.  Проанализируйте этапы вычисления коэффициента дисконтирования для момента времени t = 1.

13.  Проанализируйте этапы вычисления коэффициента дисконтирования для момента времени t = 2.

14.  Проанализируйте этапы вычисления коэффициента дисконтирования для момента времени t = 3.

15.  Используя данные таблицы 21, нарисуйте и объясните зависимости значений чистой приведенной стоимости от уровня достоверности a.

16.  В чем состоит основное преимущество теории нечетких множеств перед вероятностным подходом?

17.  Какими возможностями обладает программный продукт Fuzzy for Excel для практического использования теории нечетких множеств?

После ответа на контрольные вопросы по теме 9, рассмотрим практическое применение аппарата нечетких множеств в расчетах управления запасами.

Пример практического применения нечетких чисел

Известны значения стоимости перевозки С₁, стоимости хранения единицы запаса в единицу времени С_s, величины спроса N (единиц запаса в течение полного времени q), число единиц запаса в партии поставки n. Первоначальный уровень запаса S₀ обеспечивает бездефицитную работу системы управления запасами в течение времени Т₁ – рис.15.

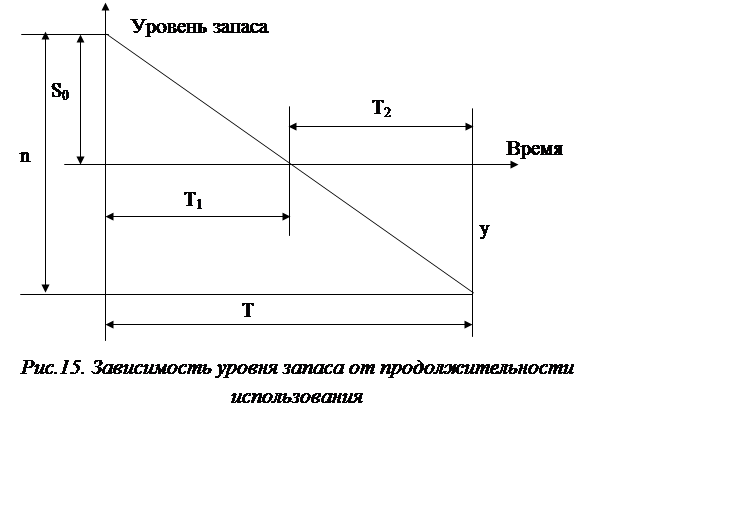Образование дефицита запаса в количестве у происходит в течение времени Т₂, поэтому время возобновления поставок Т = Т₁ + Т₂. Для нормальной работы системы значение n > S₀. Найти оптимальные значения n*, S*₀, T* и величину общих затрат D* системы управления запасами.

Решение

1. Общие затраты складываются из транспортировки продукции (С_s), хранения (в течение времени Т₁), прекращения выпуска продукции (в течение времени Т₂):

D(n,S₀) = 0,5×[ S₀×T₁× С_s + С₁ + (n -S₀)×T₂×С_p]×N/n               (1)

2. Из рис.15 видно, что:

Т₁ / T = S₀ / n

T₂ / T = (n – S₀) / n                       (2)

3. Теперь формула (1) будет записана:

D(n,S₀) = 0,5×S²₀×q×С_s/ n + N×С₁ / n + 0,5×(n – S₀)²×q× С_p / n (3).

4. Взяв частные производные от функции (3) по переменным n и S₀, приравниваем их к нулю и получаем оптимальные значения:

n* = n₁/A                                                  (4)

S*₀ = n₁×A                                                 (5)

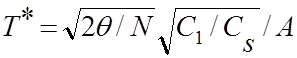                       (6)

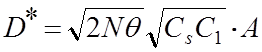                            (7)

В этих выражениях 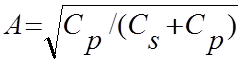         (8)

Значение величины         (9)

5. Учитывая, что С₁, С_s, С_p – нечеткие треугольные числа, используем формулы (4 – 7) для получения трехмерных массивов данных. Так, например, для С₁(200000, 300000, 370000), С_s(3, 3.5, 4.4), С_p(20, 35, 40) и N = 120000 единиц поставок в течение года (q = 360 дней), получим следующие результаты – табл. 32.

Таблица 32

Результаты расчета системы управления запасами

Мы неслучайно сначала показали полученные результаты, но не сказали, насколько трудоемки такие расчеты. Приведем их полностью.

Как видно из приведенных формул значения С₁, С_s, С_p – нечеткие треугольные числа. Это значит, что каждое из них имеет значения левой, правой границ и наиболее вероятное значение. Для нечетких треугольных чисел:

С₁= (С₁₁, С₂₁, С₃₁);

С_s = (С_1s, С_2s, С_3s);

С_p = (С_1p, С_2p, С_3p).

С учетом этого, вначале должны быть рассчитаны значения С₁, С_s, С_p для каждого уровня a - сечений. Формулы для расчета этих значений:

С₁ = {[ С₁₁ + a×( С₂₁-С₁₁)],[ С₃₁ - a×( С₃₁-С₂₁)]}         (10)

С_s = {[ С_1s + a×( С_2s-С_1s)],[ С_3s - a×( С_3s-С_2s)]}           (11)

С_p = {[ С_1p + a×( С_2p-С_1p)],[ С_3p - a×( С_3p-С_2p)]}         (12)

Только теперь можно подсчитывать значения частных и произведений по следующим формулам:

С₁(×)С_s={[С₁₁+a×(С₂₁-С₁₁)]×[С_1s+a×(С_2s-С_1s)],[С₃₁-a×(С₃₁-С₂₁)]×[С_3s -a×(С_3s-С_2s)]}                                     (13)