Математические методы теории принятия решений: Курс лекций, страница 16

Сформулированная задача оптимизации максимального накопления капитала (1) - (5) вычисляет траекторию оптимального роста на длительные сроки – в среднем 5 - 15 лет. По окончании расчета на печать выводятся значения исходных данных: величина расчетного периода; матрицы коэффициентов  и ; первоначальные значения  объемов выпуска; оценки запасов ресурсов. Итоговые результаты оптимизации включают: значения добавленной стоимости; величины объемов выпуска (по годам); значения нормы прибыли (по годам).

Как видим, и здесь используется хорошо отработанный теоретически и многократно проверенный материал ЛП в практической деятельности многочисленных фирм, промышленных объединений и других экономических объектов у нас и за рубежом.

Динамическая оптимизационная модель потребления

В предыдущей модели максимального накопления капитала в конце планового периода решалась многоразмерная задача. При изучении данных экономики одной из стран за 10-летний период, потребовалось 52 итерации. То есть сам процесс расчета продолжался (даже при использовании современного компьютера) несколько часов. Для получения надежных результатов расчеты ведут с двойной точностью.

В предыдущей задаче само накопление капитала являлось единственным ограничением экономического роста.

Максимум суммы накопленного капитала составил  денежных единиц [4].

В динамической оптимизационной задаче потребления ограничение роста уровня потребления связывается с приростом активно работающего населения (т.е. с трудовыми резервами). Это значит, что темпы прироста производительности труда  связываются с приростом работающего на производстве населения по формуле:

,

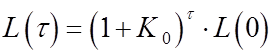где  - первоначальное количество занятых в процессе производства.

И в этой модели (максимального потребления) математический аппарат аналогичен уже рассмотренному.

1. Обычная векторная форма связи "затраты – выпуск":

,

где  - конечный спрос (потребление) зависит от уровня потребления и доходов (инвестиций).

2. Связав коэффициенты потребления с конечным продуктом, т.е. функцию потребления  с добавленной стоимостью, устанавливают зависимость величины потребления от объемов выпуска: .

3. Предположив, что темпы прироста всех материальных благ  одинаковы, получаем связь объемов выпуска по времени с темпами прироста  в векторной форме:

(E – A)BX(t) = X(t) / m.

Добавляются те же ограничения (2) - (5), и решается задача оптимального потребления по тому же сценарию, что и в оптимизационной задаче максимального накопления капитала.

И в этом случае на печать выводятся аналогичные исходные данные и итоговый результат. Для трех агрегированных отраслей экономики при плановом периоде 5 лет число итераций составило 33, а продолжительность расчета около 10 минут [4]. Результаты расчета показали, что объемы продукции первой отрасли уменьшились на 10,3%; второй – возросли на 47%, третьей – возросли на 57,3%, а рост общего объема выпуска продукции составил 46,5%. За этот же период величина потребления возросла на 58,1%.Максимальное значение целевой функции (общая сумма потребления) составило  денежных единиц.

Контрольные вопросы к теме №3

1.  Охарактеризуйте структуру и тип целевой функции и ограничений в оптимизационной задаче Леонтьева.

2.  Назовите основные этапы информационной технологии моделирования для модели Леонтьева в методе «затраты – выпуск».

3.  Почему алгебраическое соотношение X_i = Sa_ij×X_j + y_i называется основным для межотраслевого баланса национальной экономики?

4.  Экономический смысл коэффициентов прямых материальных затрат в межотраслевом балансе.

5.  Экономический смысл коэффициентов полных материальных затрат в межотраслевом балансе.

6.  Достоинства и недостатки при различных способах задания исходных данных в статическом межотраслевом балансе.

7.  Что показывает сопоставление двух первых квадрантов статического и динамического межотраслевого баланса?

8.  Назовите основные этапы информационной технологии моделирования для статического и динамического межотраслевого баланса.