Математические методы теории принятия решений: Курс лекций, страница 12

Решение этой задачи позволяет обнаружить точку Е(2,6; 5). Это значит, что величина F₂ = 2,6 + 5 = 7,6. Именно эта прямая и проходит через точку Е. Провести ее на рис.3 можно следующим образом. При x₂ = 0 значение x₁ = 7,6. Через две точки Е(2,6; 5) и М(7,6; 0) можно провести прямую и притом только единственную. Теперь область допустимых решений изменилась, она обозначена ABELDA. Причем координаты всех точек известны: для точки L(4; 3,6); для точки
D(4; 1); для точки K(4; 4,3); для точки E(2,6; 5). Координаты точек А и В видны на рис.3: координаты точки А(0; 3), координаты точки В(0;5).

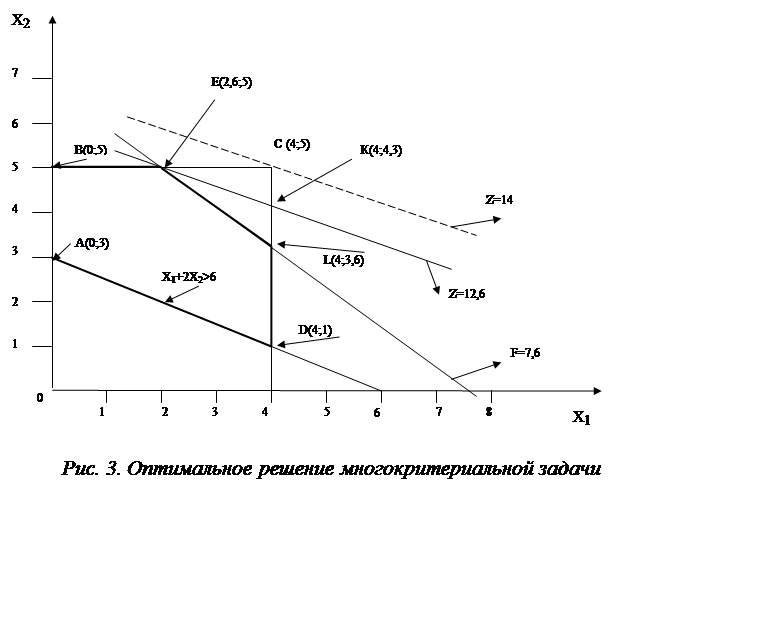Итак, компромиссный план для двух критериев обеспечивает: максимум дохода в количестве 12,6 денежных единиц, минимум издержек производства в количестве 7,6 денежных единиц. Координаты точки оптимума Е(2,6; 5).

Пример задачи был выбран с двумя переменными только для того, чтобы визуально убедить в правильности действия алгоритма. Ясно, что принцип решения многокритериальных задач со множеством переменных и ограничений будет таким же. И тогда не потребуется рисунок. Кроме того, при числе переменных больше трех изобразить его невозможно.

Контрольные вопросы к теме №2

1. Как связаны термины «многокритериальности» с показателями реальной экономической действительности?

2. Почему нельзя судить об эффективности работы двух предприятий по разным критериям?

3. В чем именно заключается одинаковость методологии поиска наилучшего результата в одно – и многокритериальных задачах?

4. Каков общий алгоритм поиска наилучших решений в многокритериальных задачах?

5. Проиллюстрируйте технологию поиска многокритериальной задачи на конкретном примере.

6. Как практически реализовать в Excel технологию поиска многокритериальной задачи на конкретном примере?

7. На приведенном в тексте примере многокритериальной задачи объяснить содержание семи этапов информационной технологии моделирования. (Содержание семи этапов приведено во введении).

Ответив на все контрольные вопросы к теме 2, следует самостоятельно решить следующую задачу, обязательно сопроводив ее соответствующим рисунком.

Дополнительная задача

Предприятие изготавливает два вида продукции. Для этого используется оборудование четырех типов: первого - не менее
12 единиц мощности; второго - не более 10; третьего - не более 6, а четвертого – не более 7 единиц мощности.

Затраты мощности оборудования каждого типа на единицу продукции первого вида составляют: 3, 1, 1, 0; затраты для продукции второго вида – 4, 1, 0, 1.

Прибыль от сбыта единицы продукции первого вида составляет три денежные единицы, второго вида – пять денежных единиц, а величина чистого дохода равна, соответственно, трем и одной денежной единице на единицу продукции.

Необходимо предложить такой план производства продукции, чтобы наиболее предпочтительным был критерий прибыльности с отклонением от своего максимального значения не более двадцати процентов.

Отклонение от максимума чистого дохода не должно превышать 40%. Менее предпочтительным критерием будут считаться затраты.

Для решения этой задачи необходимо выполнить следующие указания:

1.  Тщательно изучить весь материал по теме 2;

2.  Представить сначала графическое решение задачи в системе координат: X₁ – горизонтальная ось; X₂ – вертикальная ось;

3.  Выполнить решение задачи с помощью технологии Excel, объяснив возможные причины расхождения результатов графического и компьютерного решения;

4.  Объяснить полученные результаты для управления планом развития производства.

ТЕМА 3. СОВОКУПНОСТЬ ВЗАИМОСВЯЗАННЫХ ОТРАСЛЕЙ ЭКОНОМИКИ

Лекция 3. Совокупность взаимосвязанных отраслей в экономике

Анализ взаимодействия системы отраслей по методу «затраты – выпуск» Леонтьева выполнен в учебном пособии [3]. Напомним, что речь идет о не оптимизационной модели. Эта модель также позволяет учитывать последствия экономической деятельности – загрязнение окружающей среды [2].

Напомним основные соотношения для совокупности взаимосвязанных отраслей экономики – статического межотраслевого баланса.