Натурное моделирование является результатом обработки наблюдений над объектами экономики и рассматривается как исходные данные для последующего математического моделирования. Информационные ресурсы математического моделирования дают знания о конкретном объекте экономики.
Весь лекционный материал десяти тем целесообразно разбить на 4 блока по 2 - 3 лекции в каждом.
Первый блок. Математические основы поиска наилучших решений в объектах микро - и макроэкономики. Оптимизация с целочисленными, булевыми и дискретными переменными. Информационные ресурсы двойственных задач (Тема 1).
Математические основы поиска наилучших решений в многокритериальных задачах. Применение технологии Excel для поиска информационных ресурсов (Тема 2).
Второй блок. Математические основы поиска наилучших решений для развития макроэкономических объектов. Межотраслевые связи в модели Леонтьева. Динамические модели развития системы отраслей. Модели накопления капитала и потребительского спроса при ограниченных трудовых ресурсах (Тема 3).
Модели оптимизации и развития производства. Математические
основы поиска наилучших решений методом неопределенных множителей Лагранжа.
Задачи оптимизации производства и трудовые ресурсы. Динамическая модель
экономического развития Солоу
(Тема 4).
Третий блок. Математические основы поиска наилучших решений во внешнеэкономической деятельности государства. Учет товарно–географической структуры импорта и экспорта. Оптимизация внешнеторгового оборота. Организация производства на импортно–экспортной основе (Тема 5).
Четвертый блок. Математические основы поиска наилучших решений в инвестиционной деятельности государства для экономики любого масштаба. Рыночная модель инвестиционной деятельности (Тема 6).
Модель совместных инвестиционных и производственных программ в предпринимательской деятельности (Тема 7).
Организация предпринимательства в условиях первоначальной нехватки денежных средств и необходимости развития производства. Конкурс инвестиционных проектов (Тема 8).
Необходимость использования аппарата теории нечетких множеств (ТНМ) менеджером для специфичных ситуаций в экономике. Универсальное множество и подмножества нечетких чисел. Основные особенности и области применения аппарата ТНМ - в том числе в инвестиционном менеджменте. Программный продукт Fuzzy for Excel (Тема 9).
Поиск наилучших решений методами динамического программирования (Тема 10).
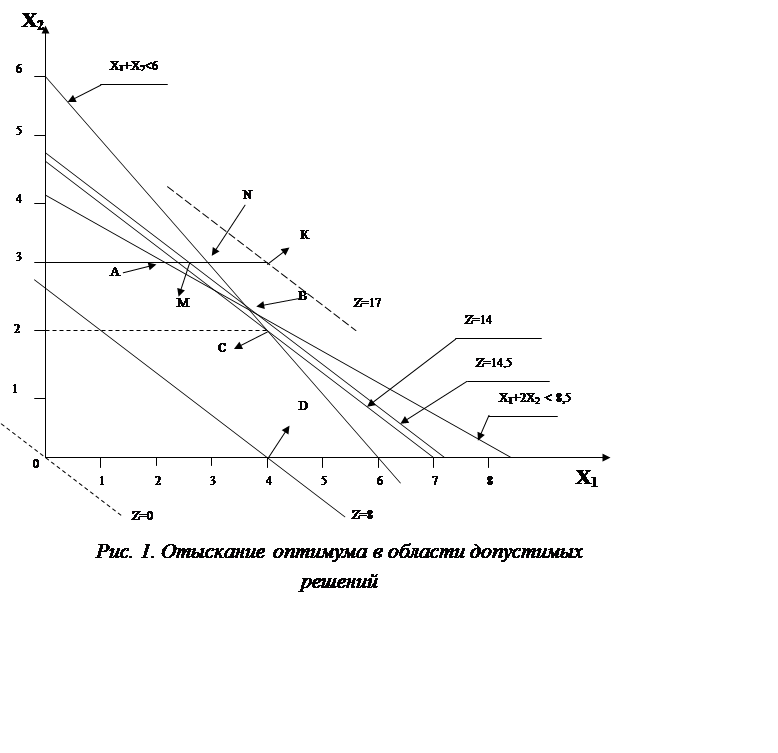
Пусть область допустимых решений (ОДР), в которой отыскивается наилучшее решение для целевой функции, определена соотношениями:
Z = 2x1 + 3x2 ® max
x1 + x2 £ 6 (1)
x1 + 2x2 £ 8,5 (2)
 x1 £ 4 (3)
x1 £ 4 (3)
x2 £ 3 (4)
 |
Ясно, что минимальное значение для целевой функции (для неотрицательных x1, x2) находится в начале координат (рис.1). Значит, для отыскания максимума целевой функции надо двигаться в плоскости (пространстве) переменных на «северо–восток». Нам придется сделать пять таких шагов.
Первый и второй шаг. Первоначальная запись целевой функции (ЦФ) и ограничений (1-4) можно представить в канонической форме:
Z=2x1 + 3x2 ® max или Z=2x1 + 3x2 ® max
x1 + x2 + x3 = 6 (1) x3 = 6 – x1 – x2 (1)
x1 + 2x2 + x4 = 8,5 (2) x4 = 8,5 – x1 - 2x2 (2)
x1 + x5 = 4 (3) x5 = 4 – x1 (3)
x2 + x6= 3 (4) x6 = 3 – x2 (4)
В этих выражениях x1, x2 называются свободными, а x3, x4, x5 и x6 – базисными переменными. Базисное решение определяется, когда движение на «северо–восток» начнется из начала координат – то есть при x1 = 0 и x2 = 0. Тогда значения x3 = 6, x4 = 8,5, x5 = 4, x6 = 3. При этом Z = 0; увеличим его за счет x1.
Третий шаг. Увеличивать x1 можно до
тех пор, пока базовая переменная x5 не станет равной нулю. Из (3)
следует, что значение
x1 = 4 – x5.
Подставив это значение в правый столбец соотношений
(1-4), получим:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.