Промышленность \ Добыча, хранение и транспортировка нефти и газа

Физические методы переработки и использования газа: Учебное пособие, страница 70

Определение дроссель-эффекта расчетным методом или по номограммам может давать значительные по­грешности, особенно при определении а\ для газов га-зоконденсатных месторождений. В этом случае более надежны экспериментальные данные.

Пример. Определить коэффициент Джоуля—Томсона для при­родного газа, состоящего из 94,5%—СН4, 2,6% — С2Не, 1,3% — С3Н8, 0,5%—С4Ню, 1,1 %— N2, при давлении 10 МПа и темпера­туре 20 °С.

1. Определяем критическое    давление и температуру    смеси рКр = 0,945-4,49 + 0,026-4,72 + 0,013-4,12 + 0,005-3,67 + + 0,011-3,28 = 4,473 МПа;

152


-

1

1

:

II |\

IJ \\

М V

ш

/I л*

N

3 V В 810

0,60,81

2  J

1200

280

168 126

0M2

0,01 0,02 0,03   0,06 0,10 -^0,2 0,3  0,6 0,8 1,0


J h   6Pn


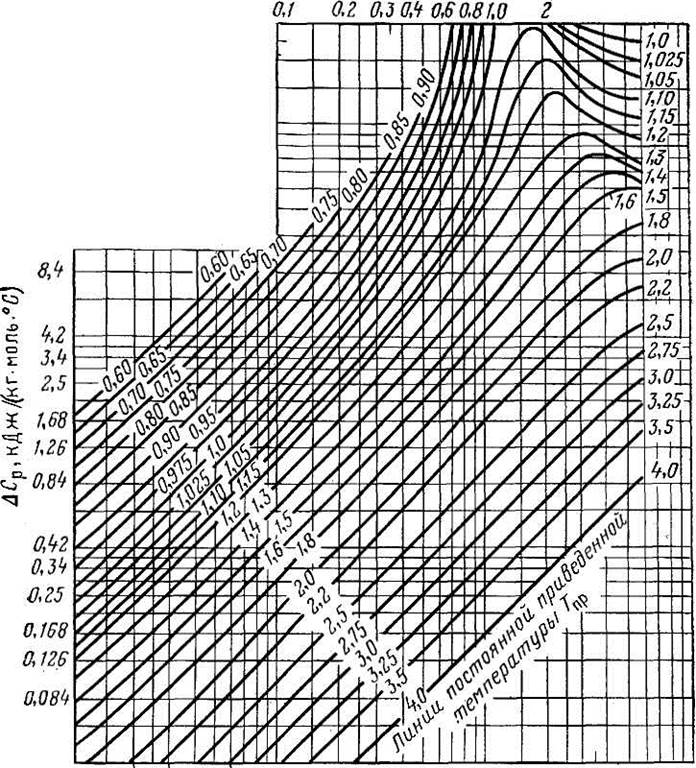
Рис. VI. 12. Поправка на изобарную   теплоемкость природного газа в зависимости от приведенных давления и температуры.

Гкр = 0,945-191,1 +0,026-305,5 + 0,013-370,0 + + 0,005-425,2 + 0,01 Ы26,2= 196,95 К.

2. Определим приведенные давление и температуру

Г         293'15      , ,о

7 ттп — . _, . . = 1,49.

пр

223

196,95

4,473

3. Используя рис. VI. 11 определяем теплоемкость газа в идеаль­ном состоянии:

сор = 0,945-36,03 + 0,026-55,73 + 0,013-76,65 + + 0,005-100,98 + 0,011-28,07 = 37,31 кДж/(кг.моль.°С).

153


4.  По рис. VI. 12 определим поправку на изобарную теплоем­
кость Аср = 15,08 кДж/(кг-моль-°С).

5.  Определяем по рис. VI.10 обобщенную функцию f (£>г) == 1,05.

6.  Определяем коэффициент Джоуля—Томсона

196,95

^1054

щ = -^-^-------------------------- 3,69° С/МПа

1        37,31 + 15,08

(4,187— переводной коэффициент давления из Джоулей в калории).

Изоэнтропийныйпроцесс

Более эффективным по сравнению с изоэнтальпий-ным (снижение температуры газового потока) является изоэнтропийный процесс расширения газа. При этом га­зовый поток при своем расширении совершает внешнюю работу в детандерах поршневого или турбинного типа.

Из общих положений термодинамики можно найти дифференциальный эффект изменения температуры при изоэнтропийном расширении:

дТ\(dS/dP)T

Поскольку (dS/dT)p = cp/T и с учетом соотношений Максвелла (dSfdp) T = — (dV/dT)p, имеем

 ■         (VU4)

Для идеального газа ср = ср0 и (dVjdT)p = Rlp,   по­этому

ид5    ср р        К    р

Сравнивая уравнения (VI.8) и (VI. 14), получаем:

 (VIЛ 6)

т. е. дифференциальный эффект изменения температуры при изоэнтропийном расширении газа всегда больше аналогичного коэффициента при изоэнтальпийном рас­ширении газа. Таким образом, использование в промыс­ловых условиях изоэнтропийного расширения газа поз­воляет более эффективно использовать пластовую энер­гию природного газа.

154


Скачать файл