vndS = \pPdV -\VndS + ]rndS. (8)
Va s V s s
Третьим фундаментальным законом гидрогазодинамики является закон сохранения энергии, который обычно формулируется в следующем виде: "Изменение энергии некоторой массы флюида за некоторый промежуток времени равно работе всех сил, приложенных к данной массе флюида за данный промежуток времени, плюс количество тепла, которое получит данная масса флюида за тот же промежуток времени вследствие процессов немеханического характера, например, теплопроводности, теплоотдачи, химических реакций и т.д." Ниже будет представлен наиболее простой вывод уравнения сохранения энергии [5,10]. Изменение энергии в единицу времени (производная от энергии по времени) может быть выражено аналогично предыдущему:
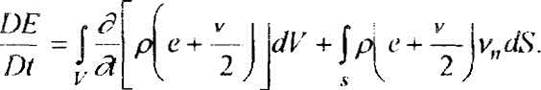 (9)
(9)
Здесь первый интеграл .выражает изменение энергии массы флюида, содержащейся в объеме V, в единицу времени при неизменности этого объема, второй - изменение энергии рассматриваемой массы флюида в единицу времени за счет переменности объема V.
Выясним, какую работу производят силы, действующие на рассматриваемую массу флюида.
Рассмотренные ранее силы производят в единицу времени следующую работу:
- f р(п- v)dS - работа сил давления;
j (тп v yiS - раоота сил трения ЫF• v\dV - работа массовых сил.
V
Если обозначить через Q вектор потока тепла, проходящего через единицу поверхности внутрь объема V в единицу времени, а через 8 - количество тепла, выделяемого единицей массы флюида за единицу времени., то получим, что \Q,,dS + jpBdV и есть количество тепла, получаемого данной массой флюида в единицу времени, где Оп- проекция вектора О на внутреннюю нормаль п к элементу dS Согласно закону сохранения, с учетом формулы (8), имеем
г 'Я f v* \\ . : v2 ■
\ —I d е + — I \dV + \ п\ е + — ■ 1///.S =
= -j р(Я ■ v^S' + I (г„ - v)dS -
/' .v !•-■■
Уравнение (10) представляет собой интегральггую форму закона сохранения полной энергии.
Интегрально-дифференциальные уравнения движения флюида в горизонтальной скважине
Приведенные выше интегральные уравнения сохранения массы, количества движения и энергии применим к движению потока флюида в горизонтальном стволе с открытой поверхностью фильтрации.
Рассмотрим для этого элементарный объем горизонтального ствола, ограниченный двумя близкими плоскими сечениями F и F| и боковой поверхностью S6oK ствола между ними (рис.1).
В соответствии с общей формой уравнения сохранения массы (2) имеем
j jvadS = 0. (11)
f sf,,,k
Здесь на поверхности
89
Fi-vn=+Vx, на F-vn=-vx, на S,,c-vn=-w, (12)
где х - ось горизонтального ствола; w - скорость притока флюида из пласта к стенке ствола; знак минус указывает на то, что положительное направление скорости w совпадает с внутренней нормалью к поверхности.
Уравнение (11), с учетом граничных условий (12), может быть записано в следующем виде:
dV + JpvxdF-\pvJF- jpwdS = 0. (13)
Для рассматриваемого элементарного объема справедливы приближенные равенства AV = AF • Дх и ASfWK « Ax AL, где AL - элемент периметра
}}Cos{t,i
В случае канала цилиндрической формы и постоянного сечения имеем Ах = Л/; Cos(Ij) = I, L=L'.
Уравнение (13) с учетом этих соотношений можно записать в виде
| |
\
I' j L
откуда при Дх-»0 получаем ингегрально-дифференциальное уравнение сохранения массы для потока флюида в горизонтальном стволе скважины
\p ^\px\p (15)
a F (ж F ;
Для получения уравнения сохранения количества движения потока флюида в горизонтальной скважине разделим правую и левую части уравнения (8) на Ах.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.