Обеспечение занятости в регионе через совершенствование управления персоналом на градообразующем предприятии, страница 16

К основным проблемам построения группировок необходимо отнести определение количества групп в группировке и разбивку имеющейся исходной информации на группы. В экономической литературе для решения данных проблем предложен ряд различных подходов. Так, для определения количества групп в группировке предлагаются, например, эмпирические формулы, таблицы, логические предпосылки [10, с. 87; 46, с. 86; 110, с. 49; 126, с. 103] и т. п.

В практике экономического анализа используются различные показатели определения однородности информации в группе и методы их образования. Так, например, В. И. Сиськов показателем однородности информации в группе предлагает считать коэффициент вариации. Информация в группе признается однородной, если значение коэффициента вариации меньше или равно 0,33 [117, с. 101].

Исходная информация о факторах, представленная количественными показателями, может разбиваться на группы с помощью ряда других формальных методов, например, V(r)²-критерия [46, с. 82], метода распознавания образов [37, с. 126], кластерного анализа [36, с. 50], метода главных компонентов                     [34, с. 139] и т. д.

При группировке и анализе информации о факторах, собранной с помощью анкет, используется   м е т о д   г р а ф к о р р е л я ц и и. Так как анкета состоит из вопросов-градаций, то анализируемый массив информации представляется в виде симметричной матрицы , где  – численность анкетируемых, одновременно отвечавших на  и  градации вопросов. На основе матрицы  вычисляются коэффициенты ρ_ij между количеством анкетируемых, ответивших на две градации вопросов анкеты [63, с. 53-58; 110, с. 80-87]:

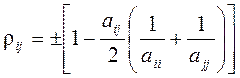                                           ,                                     (1.2)

или в более точной форме –

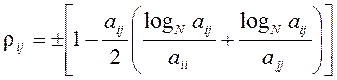                                   ,                            (1.3)

где N – количество анкетируемых.

Величина коэффициента корреляции ρ_ij колеблется в интервале  0 – 1. Сильная корреляционная связь проявляется в случае, если все опрашиваемые отвечают ρ_ij одновременно на вопрос, или когда , тогда ρ_ij равно нулю или его величина близка к нулю. Если же , то , ρ_ij = 0, что характеризует отсутствие корреляционной зависимости. Матрица коэффициентов ρ_ij представляет исследуемый массив в виде полного симметричного неориентированного связанного графа G, где множество вершин G являются градациями социально-экономической анкеты.

Поэтому для оценки степени тесноты и направления корреляционной связи между показателями занятости , факторами  и между самими факторами  используется  корреляционный м е т о д. Имеющаяся исходная информация ( и  представлены дискретными или интервальными величинами, даны единичные или групповые значения, представлены количественными или качественными показателями и т. д.) обусловливает выбор коэффициента, характеризующего корреляционную связь. Наиболее широко при изучении влияния факторов на динамику показателей занятости для определения корреляционной связи используются:

– коэффициент корреляции знаков Г. Фехнера;

– коэффициенты контингенции (К_к) и ассоциации (К_а)  при наличии таблицы четырех полей;

 – биссериальный коэффициент К, позволяющий определить наличие корреляционной связи между количественными и качественными признаками;

– коэффициент взаимной сопряженности Пирсона (К_п)  характеризующий наличие корреляционной связи между показателями (количественными, качественными или количественными и качественными одновременно);

– линейный коэффициент корреляции , показывающий тесноту связи между двумя рядами количественных показателей:

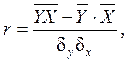                                                                                                   (1.4)

;

;

;

;

;

                       

;   ;

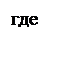
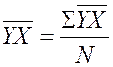
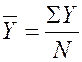
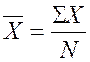
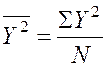
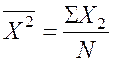
N – количество наблюдений.

Для оценки статистической достоверности коэффициента линейной корреляции рассчитывается t-критерий Стьюдента:

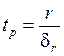                                                             ,                                               (1.5)

где

.

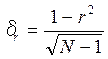Если , то влияние исследуемого фактора на показатель занятости следует признать существенным при данном уровне значимости. При величине линейного коэффициента корреляции 0,10–0,30 связь между показателем занятости и (или) факторами считается слабой, при r = 0,31 … 0,50 – умеренной, r = 0,51 … 0,70 – заметной, r = 0,71 … 0,90 – тесной, r = 0,91 … 0,99 – весьма тесной.

Для определения корреляционной связи используется ряд других показателей: биссериальный коэффициент корреляции, коэффициенты Чупрова, Кендалла и т. д. [45, с. 640, 746; 110, с. 88; 126, с. 470].

Однако использование вышеперечисленных коэффициентов является половинчатой мерой, т. к. они свидетельствуют только о наличии корреляционной связи между изучаемыми явлениями (показателями занятости и взаимосвязям между самими факторами). На основе анализа матрицы коэффициентов парной корреляции осуществляется отбор показателей для включения в регрессионные модели.

В социально-экономических исследованиях наиболее часто используют многофакторные регрессионные модели линейного вида

                                              ,                              (1.6)

где а₀ – свободный член регрессионного уравнения;

а₁ – коэффициент регрессии, характеризующий изменение показателя занятости при изменении фактора на единицу своего натурального выражения;

Х₁ – фактор – социально-экономический, экологический, правовой и т. д. показатель.