3) максимальной и минимальной точки;
4) предусматривающий анализ линейной зависимости между выручкой от реализации и совокупными затратами;
5) наименьших квадратов;
6) упрощённый статистический.
Метод анализа счетов предполагает разделение затрат на основе интуиции и опыта контроллера в результате наблюдения за динамикой затратных показателей в предыдущие периоды.
Визуальный метод предусматривает построение графика, приблизительно отображающего наличие связи между затратами и объёмом произведённой продукции. Для этого на координатную плоскость (рис. 2.1) наносятся точки, характеризующие динамику затрат и объёмного показателя на протяжении всего анализируемого периода времени. В дальнейшем исследователь должен провести прямую, которая, на его взгляд, наиболее адекватно отобразит поведение затрат. Точка пересечения прямой и оси ординат позволяет оценить примерную величину постоянных затрат.
Метод максимальной и минимальной точки основывается на использовании крайних значений объёма произведённой продукции. При этом ставка переменных затрат может быть определена с помощью следующей формулы:
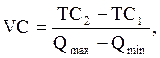
где VC – удельные переменные затраты; TC2 – величина общих затрат, соответствующих максимальному значению объёмного показателя; TC1 – величина общих затрат, соответствующих минимальному значению объёма произведённой продукции; Qmax – максимальный объём произведённой продукции; Qmin – минимальный объём произведённой продукции.

Рассмотренный метод рекомендуется
использовать, по мнению авторов пособия, в тех случаях, когда удельные
переменные затраты остаются неизменными при увеличении или уменьшении объёма
произведённой продукции. Иными словами, речь идёт о случаях, когда существуют
так называемые пропорциональные переменные затраты.
Метод, предусматривающий анализ линейной зависимости между выручкой от реализации и совокупными затратами, основан на решении системы уравнений. Причём для поиска решения для случая с N видами продуктов потребуется N+1 период наблюдений.
В этом случае искомая система уравнений, связывающая затраты и выручку, примет следующий вид
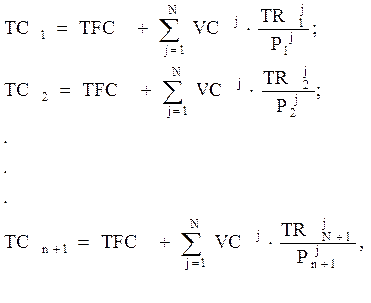
где TC1, TC2, TCn+1 – совокупные затраты
соответственно в первый, второй и (n +
1)-й периоды наблюдений; TFC
– совокупные постоянные затраты; VCj – удельные переменные затраты, связанные с производством и
реализацией j-й продукции; ![]() – выручка от реализации продукции j соответственно в первый, второй и (n + 1)-й периоды наблюдений;
– выручка от реализации продукции j соответственно в первый, второй и (n + 1)-й периоды наблюдений; ![]() – цена единицы j-й продукции соответственно в первый, второй и (n + 1)-й периоды наблюдений; N –
общее количество наименований продукции, реализуемой на протяжении n + 1 периода.
– цена единицы j-й продукции соответственно в первый, второй и (n + 1)-й периоды наблюдений; N –
общее количество наименований продукции, реализуемой на протяжении n + 1 периода.
Представленный метод, очевидно, является весьма удобным для анализа тех случаев, когда осуществляется производство широкой номенклатуры изделий.
Метод наименьших квадратов основан на нахождении параметров прямой, проходящей таким образом, что квадрат расстояний от всех точек фактических затрат до теоретической линии затрат должен быть минимальным. В итоге ставка переменных затрат может быть определена по формуле:
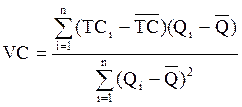 ,
,
где TCi – совокупные
затраты в i-й период наблюдений; ![]() – средние совокупные затраты,
рассчитанные для n периодов наблюдений; Qi – объём
реализации в i-й период наблюдений;
– средние совокупные затраты,
рассчитанные для n периодов наблюдений; Qi – объём
реализации в i-й период наблюдений; ![]() – средний
объём реализации, рассчитанный для n периодов наблюдений.
– средний
объём реализации, рассчитанный для n периодов наблюдений.
Для практических вычислений целесообразным видится применение функции Microsoft Excel ЛИНЕЙН. Для этого в поле известного значения y (Изв. знач. у) необходимо ввести множество значений ряда, характеризующего динамику совокупных затрат. В свою очередь, в поле известного значения х (Изв. знач. х) необходимо указать множество значений ряда, отражающего динамику выручки.
Упрощённый статистический метод Н.Г. Чумаченко базируется на расчёте средних величин объёма выручки и затрат. Причём расчёт производится для двух групп показателей выручки, которые предварительно должны быть определены в результате ранжирования. В конечном счёте величина постоянных затрат рассчитывается по формуле:
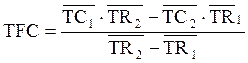 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.