Контроллинг: Учебное пособие (Сущность и организация контроллинговой деятельности. Стратегическая диагностика позиции предприятия), страница 27

Таблица 5.1

Возможные варианты факторных детерминированных моделей

В процессе моделирования факторных систем стремятся к тому, чтобы установить максимальное количество факторов, оказывающих влияние на результативный показатель. В связи с этим моделирование мультипликативных и аддитивных факторных систем осуществляется путем последовательного расчленения факторов исходной системы соответственно на факторы-сомножители или факторы-слагаемые. Что касается кратных моделей, то в отношении них применяются следующие способы преобразования: удлинение, формальное разложение и расширение /40/.

В результате удлинения факторная модель раскладывается на слагаемые. В итоге формируется конечная модель в виде выражения:

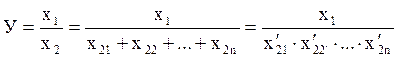, где х₂₁, х₂₂, х_2n,  – факторы, полученные в результате формального разложения факторной модели.

Использование способа расширения состоит в том, что и числитель, и знаменатель первоначальной факторной модели умножается на один и тот же показатель. Он обычно обеспечивает переход от факторов х₁, х₂   к новым факторам К₁, К₂

,

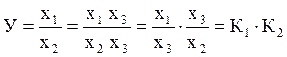Например, для анализа рентабельности активов может быть сформирована следующая факторная модель:

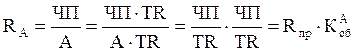,                            (5.1) где R_A – рентабельность активов предприятия; R_пр –  рентабельность продаж;  – коэффициент оборачиваемости активов предприятия.

В свою очередь, для рентабельности продаж может быть сформирована следующая факторная модель:

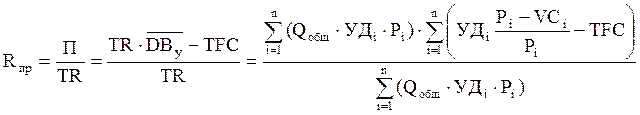, где  – средний уровень суммы покрытия по отношению к выручке от реализации; Q_общ – общее количество реализованных товаров; УД_i – удельный вес i-го вида товаров в общем объеме реализованных товаров; n – общее количество видов однородных товаров.

Из формулы (5.1) вытекает, что на рентабельность активов предприятия оказывает влияние сумма покрытия.

5.2.        Способы измерения факторов в процессе детерминированного анализа

Для оценки влияния выявленных факторов на результативный показатель может быть использован один из следующих способов:

1)  ценной подстановки;

2)  абсолютных разниц;

3)  относительных разниц

4)  пропорционального деления;

5)  индексного;

6)  интегрального.

Одним из наиболее популярных способов измерения факторов в процессе детерминированного анализа является способ ценной подстановки. Алгоритм расчета в таком случае предусматривает определение ряда значений результативного показателя с помощью соотношений:

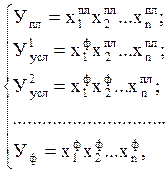                                                   (5.2)

где У_пл., У_ф – соответственно плановое и фактическое значение результативного  показателя;   – планируемые значения факторов; – фактические значения товаров;  ,  – условные значения результативных факторов.

Необходимо отметить, что с учетом условия (5.2) следует выполнить n + 1 расчет результативного показателя. При этом влияние отдельных факторов определяется в следующей последовательности:

ΔУ₁ = У¹_усл. – У_пл;

ΔУ₂ =  У²_усл. –  У¹_усл;

……………………..

……………………..    

……………………..

ΔУ_n = У_ф – У^n-1_усл, где ΔУ₁, ΔУ₂, ΔУ_n – изменение результативного показателя вследствие действия соответственно 1-го, 2-го и n-го факторов.

В процессе использования способа ценной подстановки следует придерживаться определенной последовательности проведения расчетов:

7)  во-первых, вначале необходимо учитывать изменение количественных, а затем качественных факторов;

8)  во-вторых, в случае наличия нескольких количественных и качественных факторов сначала надлежит изменить величину факторов первого уровня подчинения, и уже потом – более низкого.

В случае применения метода абсолютных разниц влияние факторов определяется путем умножения абсолютного прироста исследуемого фактора на базовую величину факторов, находящихся в факторной модели справа от него, а также на фактическую величину факторов, расположенных слева от него.