Контроллинг: Учебное пособие (Сущность и организация контроллинговой деятельности. Стратегическая диагностика позиции предприятия), страница 17

Выражение (3.2) означает, что оптимальный план производства должен отличаться ассортиментной структурой, позволяющей максимизировать сумму покрытия по предприятию в целом.

Следует отметить, что задачи максимизации суммы покрытия должны быть решены при условии соблюдения системы ограничений. В общем виде она может выглядеть так:

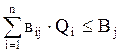  (i = 1, 2, …, m),                                            (3.3)

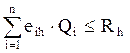  (h = 1, 2, …,k),                                            (3.4)

            (i = 1, 2, …, n),                                                (3.5)

где b_ij – расход дефицитного j-го ресурса типа В на единицу i-го товара;        m – количество наименований ресурсов типа В; В_j – количество дефицитного j-го ресурса типа В; e_ih – расход дефицитного h-го ресурса типа R на единицу  i-го товара; k – количество наименований ресурсов типа R; R_h – количество дефицитного h-го ресурса типа R.

Ограничения (3.3) и (3.4), как правило, используются для характеристики ограничивающих факторов соответственно в сфере производства и снабжения. Ограничение (3.5) задает условие неотрицательности объемов отдельных видов товаров, включенных в оптимальный план производства.

Как показывает опыт, для решения сформулированной задачи может быть рекомендовано к использованию функция Microsoft Excel «Поиск решения». Для этого необходимо составить матрицу-строку, характеризующую ассортиментную структуру плана производства. Первоначально все элементы матрицы принимаются равными нулю. Затем, используя выражения (3.2) – (3.4), в отдельные ячейки следует ввести формулы для расчета целевой функции и ограничивающих факторов. Ссылки на соответствующие ячейки необходимо указать в полях «Установить целевую ячейку» и «Ограничения». При этом в поле «Равной» следует выбрать вариант «Максимальному значению». Кроме того, в поле «Ограничения» необходимо задать условие неотрицательности (3.5). Наконец, в поле «Изменяя ячейки» необходимо указать область, которая включает ячейки, соответствующие элементам матрицы-строки. Для вывода оптимального варианта плана производства нажимается кнопка «Выполнить».

Следует обратить внимание на то, что сформулированная модель (см. формулы (3.2) – (3.5)) может быть применена только при соблюдении двух условий:

·  во-первых, целевая функция и ограничения должны быть заданы в форме линейки зависимости;

·  во-вторых, количественные ограничения на объем используемых ресурсов должны быть заранее известны.

3.3.        Принятие решений об организации собственного производства

Задача организации собственного производства является актуальной, если, во-первых, потребление анализируемых изделий осуществляется в значительном объеме, и; во-вторых, деятельность по производству этих изделий не является объектом специализации.

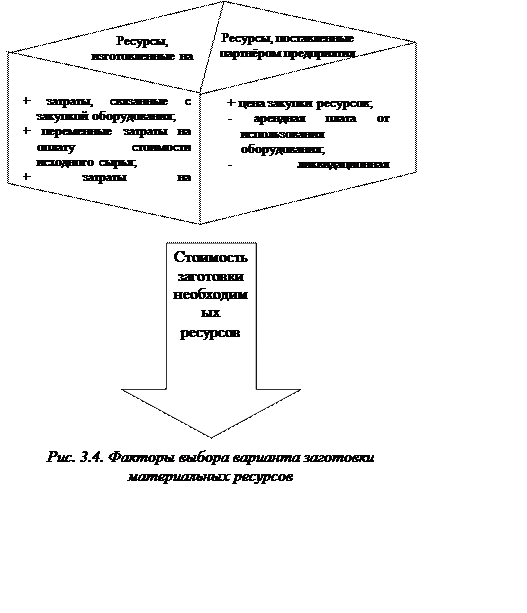
Как показывает анализ публикаций /18, 40/, наибольшие трудности при принятии решения о целесообразности организации собственного производства связаны с необходимостью сбора информации о релевантных затратах. К их числу традиционно относят затраты, приведенные на рис. 3.4.

Следует особо отметить, что представленный перечень не является исчерпывающим, а поэтому в зависимости от специфики каждой конкретной ситуации требует дальнейшей конкретизации. В связи с этим, по мнению авторов, при поиске решения необходимо учитывать следующие обстоятельства:

1)  собственное производство анализируемых изделий уже осуществляется;

2)  собственное производство анализируемых изделий до сих пор отсутствовало.

В том случае, если предприятие уже имеет опыт организации собственного производства анализируемого изделия, возможно четыре варианта развития событий (табл. 3.1). Критерием принятия управленческого решения, предусматривающего реализацию одного из вариантов, является минимум чистых релевантных затрат.

В случае отсутствия у предприятия опыта организации собственного производства анализируемого изделия предлагается рассмотреть два варианта. Выделение этих вариантов обусловлено различной степенью готовности предприятия к организации самостоятельного производства.