 Следует иметь в виду, что если в шарнирной
системе имеются статически неопределимые части, то определение nD по формуле (
1.6 ) может давать ошибку.
Например, для рамы с расчётной схемой по рис. 1.10, а получается шарнирная система, показанная на рис. 1.10, б. Для нее WШС = 2У – С
– С0 =
Следует иметь в виду, что если в шарнирной
системе имеются статически неопределимые части, то определение nD по формуле (
1.6 ) может давать ошибку.
Например, для рамы с расчётной схемой по рис. 1.10, а получается шарнирная система, показанная на рис. 1.10, б. Для нее WШС = 2У – С
– С0 = 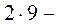 8
–
8
–
– 10 = 0, откуда nD = 0.
а) б)
Рис. 1.10


 Но
легко увидеть,
что у шар-
Но
легко увидеть,
что у шар-
нирной
системы в действительно-
сти
имеется одна степень
свобо-


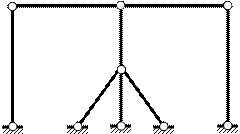
 ды ( рис. 1.11 ), то есть на самом
ды ( рис. 1.11 ), то есть на самом
деле
nD = 1,
а не 0. Причиной









 ошибки является наличие одной
ошибки является наличие одной
лишней связи в треугольной части
abcd. По
этой же причине невер-
ный
результат даст и формула ( 1.5 ), которая арифметически
и по смыслу идентична формуле ( 1.6 ).

Такого рода ошибки не возникают, если степень линейной подвижности расчётных
узлов
nD определяется
по числу
nд.с. дополнительных
линейных связей, вводимых в узлы ШС (
стр. 11
), так как
этот способ основан на
структурном анализе шарнирной системы, в отличие
от формулы (
1.6
), относящейся к
количественному анализу.
Недостатком «структурного» способа является то, что он плохо формализуется.
Используем
изложенные выше сведения для оценки степени кинематической неопределимости nk = nq + nD плоских систем. Рама, изображённая на
рис. 1.7, имеет 4 жёстких расчётных узла (А, В, С и Н),
тогда nq = nж.у. = 4. Степень линейной подвижности
узлов nD уже определена в двух вариантах – для
расчёта с учётом всех видов деформаций элементов ( в
этом случае nD = = 10 ) и без
учёта продольных деформаций стержней ( по
гипотезе ( 1.4 ) ) – nD = 2. Степень кинематической
неопределимости nk в
первом варианте получается равной 14, во
втором 6.
Рама с расчётной
схемой по рис. 1.12, а имеет продольно деформируемый элемент (
затяжку
)
и упругие связи – линейную в опорном узле
а и угловые – в верхнем узле
с
и опорных защемлениях
f и
g .
а) б)
Рис. 1.12
Число расчётных жёстких узлов
рамы nж.у. = 7 ( конструктивно жёсткие узлы e, b, d и условно жёсткие узлы f, c, g с
угловыми упругими связями, причем в с – два ), тогда степень угловой подвижности узлов nq = nж.у. = 7.
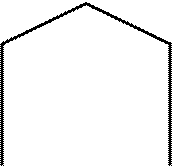
Шарнирная система, по-лученная введением цилиндрических
шарниров во все жёсткие узлы и продольного поступательного шарнира
в затяжку ( стержень, для которого нужно учитывать
продольную деформацию),
а также удалением всех упругих связей, представлена на рис. 1.12,
б. Она имеет 7 узлов a,
e, b, c,
d, g, f ( У = 7 ), 6 стержней ( bd не учитывается ) и 4
опорных связи, т.е. С = 6, С0 = 4.




Характеристика
WШС =
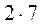
– 6 – 4
= 4, следовательно, степень линейной подвижности






узлов
nD =
WШС = 4. Такое же


значение
nD получается, если





его определять как число ли-
![]() Следует иметь в виду, что если в шарнирной
системе имеются статически неопределимые части, то определение nD по формуле (
1.6 ) может давать ошибку.
Например, для рамы с расчётной схемой по рис. 1.10, а получается шарнирная система, показанная на рис. 1.10, б. Для нее WШС = 2У – С
– С0 =
Следует иметь в виду, что если в шарнирной
системе имеются статически неопределимые части, то определение nD по формуле (
1.6 ) может давать ошибку.
Например, для рамы с расчётной схемой по рис. 1.10, а получается шарнирная система, показанная на рис. 1.10, б. Для нее WШС = 2У – С
– С0 = ![]() 8
–
8
–
![]()
![]()
![]()
![]()
![]()

 Но
легко увидеть,
что у шар-
Но
легко увидеть,
что у шар-![]()
![]()
![]()
![]() ды ( рис. 1.11 ), то есть на самом
ды ( рис. 1.11 ), то есть на самом ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ошибки является наличие одной
ошибки является наличие одной 

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()