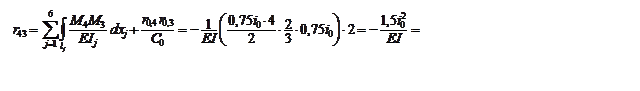
В заключение найдём
r43
«перемножением» эпюр:

Полученное значение
r43 равно
r34 – условие взаимности единичных реакций выполняется.
Для контроля правильности вычисления коэффициентов
rik производится их
универсальная проверка с помощью суммарных единичных усилий, способом
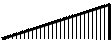 «перемножения» эпюр. Суммарная
«перемножения» эпюр. Суммарная

единичная эпюра изгибающих мо-




ментов
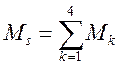
приведена
на

рис. 2.10.
При этом суммарная еди-
ничная реакция упругой связи
r0,s =
= 2
i0 . Находим обобщённую (
груп-
повую
) суммарную единичную ре-
акцию
всех введённых связей:
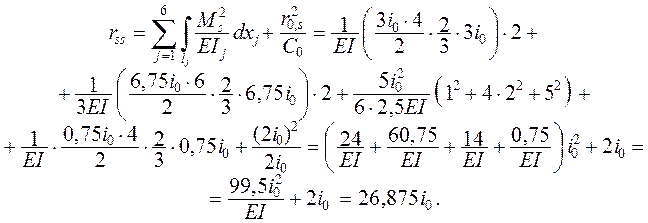 Полученный
результат должен совпасть с суммой всех коэффициентов КУМП:
Полученный
результат должен совпасть с суммой всех коэффициентов КУМП:
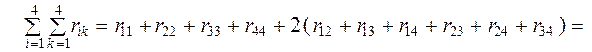
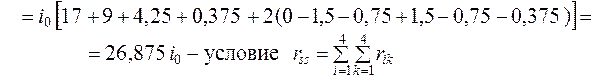
2.3.2. Определение и проверка свободных членов уравнений
Для нахождения свободных членов канонических уравнений рассматриваются
состояния основной системы, соответствующие каждому из четырёх вариантов
заданных воздействий.
При силовых воздействиях ( в первых двух
вариантах ) расчётные узлы остаются неподвижными; изгиб
стержней возникает только от внеузловых нагрузок; сосредоточенные силы и
моменты, приложенные в узлах, изгиба элементов ОСМП не вызывают. Изгибающие
моменты и поперечные силы в стержнях, рассматриваемых как независимые друг от
друга, определяются с помощью таблиц стандартных задач для типовых элементов
ОСМП ( см.
табл. 1.2 ).
1-го
( f = 1 ) варианта воздействий ( постоянной
нагрузки ), а на рис. 2.11, б, в – эпюры
изгибающих моментов и поперечных сил.
Продольные силы – постоянные по длине элементов 1, 2, …, 6 находим ( в кН ) из
условий равновесия узлов через поперечные силы ( в узле
1 учитывается нагрузка F0 ):
N1,F1 = – 12,5 ; N3,F1 = – 27,5 ;
N2,F1 = 0 ; N4,F1 = – 281,25 ;
N5,F1 = 0 ; N6,F1 = – 95.
«Грузовые» реакции связей определяем
статически – способом вырезания узлов:
R1F,1 = –75 кН* м ;
R2F,1 = 45 кН * м ; R4F,1 = 0 ;
R3F,1 = – 281,25 * cos g =
= – 168,75 кН .
|
|
На рис. 2.11, а изображена схема
деформаций ОСМП от
Mq = 60 кН * м
q =
30 кН/м
F0= 100
кН
F =
40 кН
|
|

а)



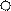




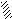

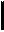





б)
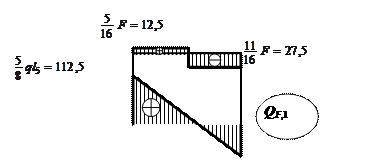



в)
От ветровой нагрузки ( 2-й вариант заданных воздействий ) ОСМП
деформируется так, как показано на рис. 2.12, а.
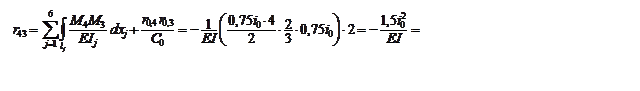
![]() «перемножения» эпюр. Суммарная
«перемножения» эпюр. Суммарная  единичная эпюра изгибающих мо-
единичная эпюра изгибающих мо-


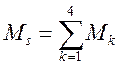 приведена
на
приведена
на
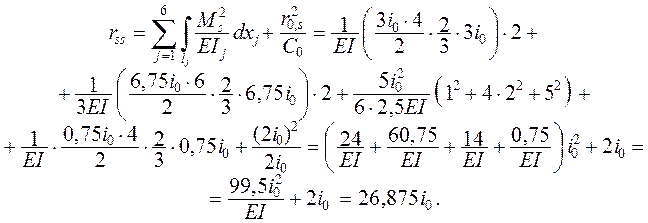 Полученный
результат должен совпасть с суммой всех коэффициентов КУМП:
Полученный
результат должен совпасть с суммой всех коэффициентов КУМП: 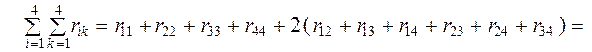
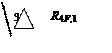






 б)
б)
 в)
в)