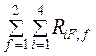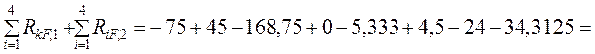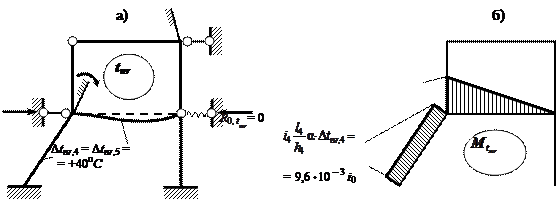Эпюры внутренних силовых факторов даны на
рис. 2.12, б, в, г . При определении изгибающих моментов и поперечных
сил используются данные табл. 1.3, а для
наклонного стержня – также схемы и формулы, приведенные на рис. 1.20. Продольные
силы и реакции линейных связей R3F,2 и R4F,2 находятся
из усло-
вий равновесия последователь-но
вырезаемых узлов 2, 3, 4, 1:
R3F,2 = – 34,3125 кН ;
R4F,2 = – 24 кН .
Реакции угловых связей
( из условий Sm = 0 для уз-
лов 1 и 3 ):
R1F,2 = – 5,333 кН * м ;
R2F,2 = 4, 5 кН * м
.
Проверку
правильности вычисления свободных членов канонических уравнений для первых
двух ( силовых ) вариантов воздействий выполним
способом «перемножения» эпюр на основании формулы ( 1.24 ), которая в рассматрива-емом
случае записывается как
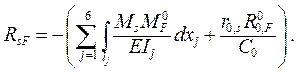 Можно проверить
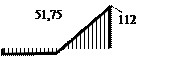
сразу все восемь найденных «грузовых» реакций – для этого к вспомогательной статически оп- ределимой системе (рис. 2.13, а) прикладываются одновременно все нагрузки 1-го и 2-го вариантов, от которых и
находятся усилия Можно проверить
сразу все восемь найденных «грузовых» реакций – для этого к вспомогательной статически оп- ределимой системе (рис. 2.13, а) прикладываются одновременно все нагрузки 1-го и 2-го вариантов, от которых и
находятся усилия 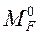 ( рис. 2.13, б ) и ( рис. 2.13, б ) и 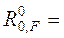 209,875 кН. 209,875 кН.
|
|
qw =
8
кН/м
;
Fw =
12
кН
;
Mw =
9
кН
*
м





















Рис. 2.13
Используя суммарную единичную эпюру Ms ( см. рис. 2.10 ) и
значение r0,s = 2i0 , вычисляем
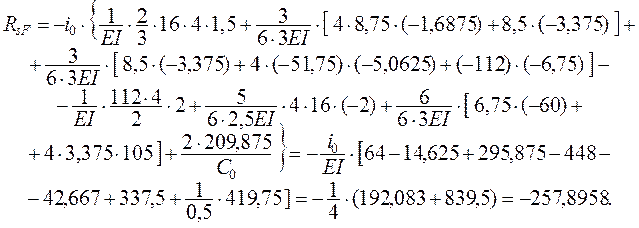 Сопоставляем полученный результат с суммой
Сопоставляем полученный результат с суммой 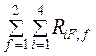
ранее
найденных свободных членов канонических уравнений
в
1-м и 2-м вариантах нагрузок:
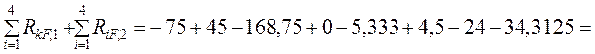
= – 257,8955 – совпадение с RsF в шести значащих цифрах.
Для отыскания реакций связей от третьего
варианта воздействий ( тепловых ) предварительно вычисляем характеристики изменения
температурного режима стержней, у которых задано изменение температуры –
неравномерные Dtnr,j и равномерные Dtj0
приращения температур по высоте сечения j-го элемента
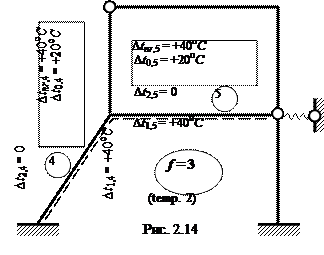
( j = 4, 5 – рис. 2.14 ): Dtnr,j = Dt1,j – Dt2,j ; Dt0j = 0,5( Dt1,j + Dt2,j ).
Деформации элементов ОСМП и соответствующие им си-
|
|
|
|
|
|
ловые факторы определяются
отдельно от приращений температур Dtnr,j и Dtj0 . От неравномерной составляющей Dtnr удлинений или укорочений
стержней не происходит, поэтому узлы основной системы не смещаются ( рис. 2.15, а ).
Изгибающие
моменты в элементах, испытывающих
|
|
|
 |
|
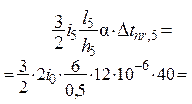
=
17,28 * 10 – 3 i0
|
|
тепловое воздействие, определяются по
табл. 1.2. В остальных стержнях моментов не возникает (
рис. 2.15,
б
).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()




![]()

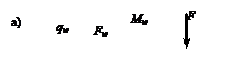
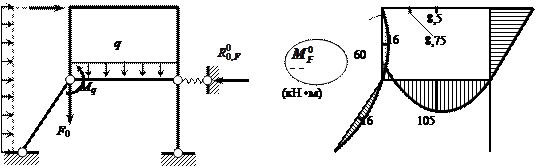
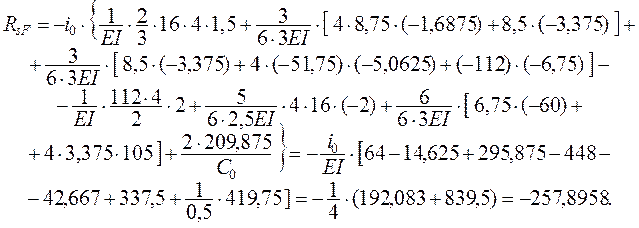 Сопоставляем полученный результат с суммой
Сопоставляем полученный результат с суммой